题目内容
两个宽度为D、质量为m的相同的小物块A、B,一带孔圆环C的质量为2m,半径为d,它们的厚度均可忽略.一不可伸长的轻质细绳绕过光滑的定滑轮,一端连接A物块,一端穿过圆环C的小孔连接B物块,如图1所示.带孔圆环C着地后C不能继续向下运动,而B能离开C继续向下运动.现将A置于水平地面,距滑轮底端3L,BC距水平地面为L,在BC的正下方有一深
、宽
d的凹槽.B、C落地后都不再弹起.
求:(1)开始运动后经多长时间带孔圆环C着地;
(2)A物块在上升的最大高度
(3)通过具体的计算分析,画出A物块在上升过程中的速度-时间(v-t)图象2.
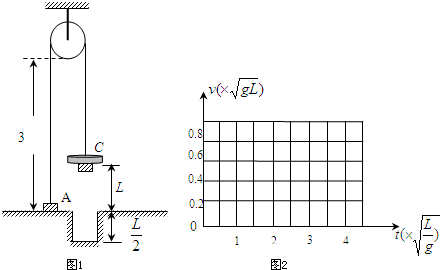
| L |
| 2 |
| 3 |
| 2 |
求:(1)开始运动后经多长时间带孔圆环C着地;
(2)A物块在上升的最大高度
(3)通过具体的计算分析,画出A物块在上升过程中的速度-时间(v-t)图象2.

分析:放手后,A、B、C整体向下做匀加速直线运动,当C被挡住后,A向上做匀速直线运动,当B到达地面后,A做竖直上抛运动,到达最高点速度减为零.结合牛顿第二定律和运动学公式求解,并作出A的速度时间图线.
解答: 解:(1)放手时,A、B、C整体的加速度:
解:(1)放手时,A、B、C整体的加速度:
a=
=
当B、C下降L时,整体的速度为:
v=
=
经历的时间为:
t1=
=2
(2)C被地面挡住后,A、B整体以v匀速运动,所用时间为:
t2=
=
当B落地后,A以v竖直向上做匀减速运动,加速度为g.
至速度减为零时,所用时间为:
t3=
=
上升高度为:
h=
g
=
A从静止上升的高度为:
H=L+
+
=2L<3L
(3)作出A的速度--时间图象,如图所示.
答:(1)开始运动后经2
时间带孔圆环C着地;
(2)A物块在上升的最大高度为2L;
(3)A物块在上升过程中的速度-时间图象如图所示.
 解:(1)放手时,A、B、C整体的加速度:
解:(1)放手时,A、B、C整体的加速度:a=
| (2m+m-m)g |
| 2m+m+m |
| g |
| 2 |
当B、C下降L时,整体的速度为:
v=
| 2aL |
| gL |
经历的时间为:
t1=
| v |
| a |
|
(2)C被地面挡住后,A、B整体以v匀速运动,所用时间为:
t2=
| ||
| v |
| 1 |
| 2 |
|
当B落地后,A以v竖直向上做匀减速运动,加速度为g.
至速度减为零时,所用时间为:
t3=
| v |
| g |
|
上升高度为:
h=
| 1 |
| 2 |
| t | 2 3 |
| L |
| 2 |
A从静止上升的高度为:
H=L+
| L |
| 2 |
| L |
| 2 |
(3)作出A的速度--时间图象,如图所示.
答:(1)开始运动后经2
|
(2)A物块在上升的最大高度为2L;
(3)A物块在上升过程中的速度-时间图象如图所示.
点评:解决本题的关键理清物体的运动情况,运用牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
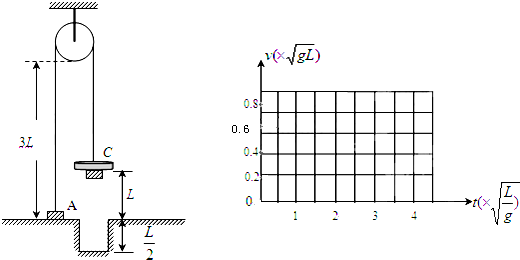
 、宽
、宽 的凹槽。B、C落地后都不再弹起。通过具体的计算分析,画出A物块在上升过程中的速度—时间(v-t)图象。
的凹槽。B、C落地后都不再弹起。通过具体的计算分析,画出A物块在上升过程中的速度—时间(v-t)图象。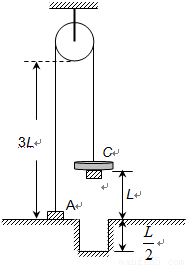
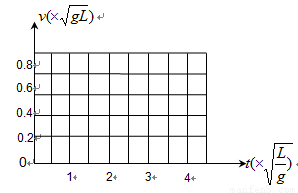
 、宽
、宽 的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。
的凹槽。B、C落地后都不再弹起。求A物块上升到最大高度所经历的时间。