题目内容
11. 如图所示,AB两端接直流稳压电源,UAB=100V,R0=40Ω,滑动变阻器总电阻R=20Ω,
如图所示,AB两端接直流稳压电源,UAB=100V,R0=40Ω,滑动变阻器总电阻R=20Ω,(1)当滑动片处于变阻器中点时,C、D两端电压为多少?通过电阻R0的电流为多少?
(2)移动滑片时,C、D两端电压最大值和最小值分别为多少?
分析 由图可知R的上端与R0串联后与R的下端并联;两支路两端的电压均为UAB,由欧姆定律可求得通过R0的电流,及R0两端的电压,当滑片移动到最上端时,CD端电压最大,当滑片移动到最下端时,此时R0被短路,CD端电压最小.
解答 解:(1)R的上半部分与R0串联的总电阻R′=R0+$\frac{R}{2}$=50Ω;
由欧姆定律可得:流过R0的电流I0=$\frac{{U}_{AB}}{R′}=\frac{100}{50}$A=2A;
R0两端的电压U0=I0R0=2A×40Ω=80V;
即CD两端的电压为80V,通过R0的电流为 2A.
(2)当滑片移动到最上端时,CD端电压最大,此时CD端的电压即为电源电压,为100V,
当滑片移动到最下端时,此时R0被短路,CD端电压最小为0,
答:(1)当滑动片处于变阻器中点时,C、D两端电压为80V,通过电阻R0的电流为2A;
(2)移动滑片时,C、D两端电压最大值为100V,最小值为0.
点评 本题主要考查欧姆定律的应用,只需明白电路结构即可顺利求解,难度不大,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
2. 如图所示,质量为m的物块在水平恒力F的推动下,从粗糙山坡底部的A处由静止运动至高为h的坡顶B处,并获得速度v,AB之间的水平距离为x,重力加速度为g,则( )
如图所示,质量为m的物块在水平恒力F的推动下,从粗糙山坡底部的A处由静止运动至高为h的坡顶B处,并获得速度v,AB之间的水平距离为x,重力加速度为g,则( )
 如图所示,质量为m的物块在水平恒力F的推动下,从粗糙山坡底部的A处由静止运动至高为h的坡顶B处,并获得速度v,AB之间的水平距离为x,重力加速度为g,则( )
如图所示,质量为m的物块在水平恒力F的推动下,从粗糙山坡底部的A处由静止运动至高为h的坡顶B处,并获得速度v,AB之间的水平距离为x,重力加速度为g,则( )| A. | 物块克服重力所做的功是mgh | B. | 合外力对物块做的功是$\frac{1}{2}$mv2 | ||
| C. | 推力对物块做的功是$\frac{1}{2}$mv2+mgh | D. | 阻力对物块做的功是$\frac{1}{2}$mv2+mgh-Fx |
19. 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图2所示,则卫星分别在轨道1、2、3上正常运行时,下列说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图2所示,则卫星分别在轨道1、2、3上正常运行时,下列说法正确的是( )
 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图2所示,则卫星分别在轨道1、2、3上正常运行时,下列说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图2所示,则卫星分别在轨道1、2、3上正常运行时,下列说法正确的是( )| A. | 卫星在轨道3上的速率大于在轨道1上的速率 | |
| B. | 卫星在轨道3上角速度的小于在轨道1上的角速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度等于它在轨道2上经过Q点时的加速度 | |
| D. | 卫星在轨道2上经过P点时的加速度小于它在轨道3上经过P点时的加速度 |
16.如图为远距离高压输电的示意图.关于远距离输电,下列表述不正确的是( )

| A. | 增加输电导线的横截面积有利于减少输电过程中的电能损失 | |
| B. | 高压输电是通过减小输电电流来减小电路的发热损耗的 | |
| C. | 在输送电压一定时,输送的电功率越大,输电过程中的电能损失越小 | |
| D. | 高压输电必须综合考虑各种因素,不一定是电压越高越好 |
3. 如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
 如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )| A. | 产生感应电动势,但无感应电流 | B. | 感应电流方向为abcda | ||
| C. | 感应电流的大小为$\frac{kπ{r}^{2}}{2R}$ | D. | 感应电流的大小为$\frac{2kπ{r}^{2}}{R}$ |
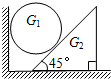 重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0,求:G1的最小值为多大时,才能使斜块滑动.
重量为G1的均匀球夹在光滑竖直平面和45°倾角的光滑斜块之间,如图所示,斜块重G2,斜块侧面与水平桌面间的摩擦系数为μ0,求:G1的最小值为多大时,才能使斜块滑动. 如图为竖直平面里有U形金属导轨,另有垂直导轨平面很大范围的匀强磁场,金属杆MN能呈水平状态导轨滑下,杆与导轨及电阻R组成闭合回路,其他电阻不计.当金属杆进入磁场后,则其运动速度图象可能是图中( )
如图为竖直平面里有U形金属导轨,另有垂直导轨平面很大范围的匀强磁场,金属杆MN能呈水平状态导轨滑下,杆与导轨及电阻R组成闭合回路,其他电阻不计.当金属杆进入磁场后,则其运动速度图象可能是图中( )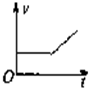



 在如图所示的电路中,A是熔断电流为2A的保险丝,R是可变电阻,S是交流电源,交流电源的内阻不计,其电动势随时间变化的规律是e=220$\sqrt{2}$sin314tV,为了不使保险丝熔断,可变电阻的阻值至少为110Ω.
在如图所示的电路中,A是熔断电流为2A的保险丝,R是可变电阻,S是交流电源,交流电源的内阻不计,其电动势随时间变化的规律是e=220$\sqrt{2}$sin314tV,为了不使保险丝熔断,可变电阻的阻值至少为110Ω.