题目内容
【题目】两个半径均为
的圆形磁场区域Ⅰ、Ⅱ相切于P点，两圆圆心分别为
、
，圆内磁感应强度分别为
、
，
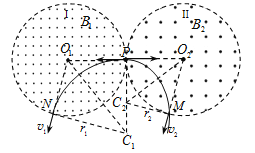
；在两圆切点P有一个静止的放射性原子核，某时刻原子核衰变成a、b两个粒子，衰变后进入Ⅱ区的粒子b从M点沿
方向以速度
射出磁场，
，如图所示；而进入Ⅰ区的粒子a从N点（图中未画出）射出磁场，且射出磁场时速度方向与同向。
（1）求a和b两粒子电荷量之比
；
（2）若a、b两粒子中有一个质量为14u，写出衰变方程，并求静止核的质量数和核电荷数；
（3）若a、b两粒子质量之比为
，求两粒子在磁场中的运动时间之比
．
【答案】（1）
；（2）
静止核的质量数为14，核电荷数为6；（3）
【解析】（1）由于
与
同向，两粒子在磁场中的运动轨迹如图所示，轨道圆心分别为
。
，由几何关系可得：
①
因此有：
②
由牛顿第二定律得：
得：
③
由于衰变中动量守恒，即：
，因此有
④
联立①②③解得 
，
⑤
（2）由粒子a的旋转方向可知其带负电，即电子，静止核发生了
衰变，新生核核电荷数为7，即氮核，所以静止核为碳核，衰变方程为：
⑦
由此可知，静止核的质量数为14，核电荷数为6；
（3）由
和
可知
⑧
代入①④⑤式及
解得
⑨
练习册系列答案
相关题目
