题目内容
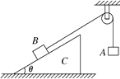
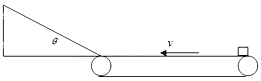
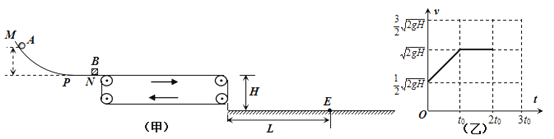
【题目】如图（甲）示，光滑曲面MP与光滑水平面PN平滑连接，N端紧靠速度恒定的传送装置，PN与它上表面在同一水平面．小球A在MP上某点静止释放，与静置于PN上的工件B碰撞后，B在传送带上运动的v-t图象如图（乙）且t0已知，最后落在地面上的E点．已知重力加速度为g，传送装置上表面距地面高度为H．
（1）求B与传送带之间的动摩擦因数μ；
（2）求E点离传送装置右端的水平距离L；
（3）若A、B发生的是弹性碰撞且B的质量是A的2倍，要使B始终落在E点，试判断A静止释放点离PN的高度h的取值范围．
【答案】）（1）
（2）
(3) 
【解析】试题分析：
（1）由v-t图象知，在t0时间内，B的加速度大小
①（1分）
B所受滑动摩擦力大小 f="2" μmg ②（1分）
又由牛顿第二定律可知B所受合力大小 f=2ma ③（1分）
解得 ：
④（1分）
（2）由v-t图象知，小球在传送带上最后的运动阶段为匀速运动，即与传送装置已达到共同速度，它从传送装置抛出的速度vB1=
, 由平抛物体运动规律：
⑤（1分）
⑥（1分）
由①②，代入vB1=，得：
⑦（1分）
（3）若使B始终落到地面上E点，也必须是以相同速度离开传送装置；设B离开传送带时的速度为
，即有
⑧（1分）
由图象可求出B在传送带上运动时的对地位移始终为
⑨（1分）
设A的质量为m，碰前速度为v，碰后速度vA；B质量为2m，碰后速度vB.
A下滑过程机械能守恒（或动能定理） mgh=
⑩（1分）
A、B碰撞过程，由A、B系统动量守恒 mv = mvA+2mvB（1分）
A、B系统机械能守恒
（1分）
联立⑩可解得
，
（1分）
B始终能落到地面上E点，有以下两类情形：
ⅰ.若
，B进入传送带上开始匀减速运动，设B减速到经过位移为S1，有
（1分），则应满足
联立①⑧⑨式，可得
（1分）
ⅱ.若
，B以速度vB进入传送带上匀加速至，设此过程B对地位移为S2，有
（1分），且恒有
联立①⑧式，得
（1分），即
恒成立，
综上所述，要使工件B都落在地面的E点，小球A释放点高度h必须满足条件：
（1分）
【评分说明：①②③④⑤⑥⑦⑧⑨⑩各1分，共18分。】
