题目内容
16.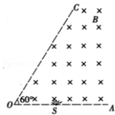 如图所示,边界0A与OC之间分布有垂直纸面向里的匀强磁场,边界OA上有一粒子源S.某一时刻,从S平行于纸面向各个方向发射出大量带正电荷的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间后,有大量粒子从边界OC射出磁场.已知∠AOC=60°,0S间距为l,从边界0C射出的粒子在磁场中运动的最短时间等于$\frac{1}{6}$T(T为粒子在磁场中运动的周期),则下列说法错误的是( )
如图所示,边界0A与OC之间分布有垂直纸面向里的匀强磁场,边界OA上有一粒子源S.某一时刻,从S平行于纸面向各个方向发射出大量带正电荷的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间后,有大量粒子从边界OC射出磁场.已知∠AOC=60°,0S间距为l,从边界0C射出的粒子在磁场中运动的最短时间等于$\frac{1}{6}$T(T为粒子在磁场中运动的周期),则下列说法错误的是( )| A. | 一定有粒子从0点经过 | |
| B. | 粒子运动轨迹和0C边界的交点到0点的最远距离为2l | |
| C. | 粒子在磁场中的运动时间可能为$\frac{1}{4}$T | |
| D. | 粒子在磁场中的运动时间可能为$\frac{2}{3}$T |
分析 从边界0C射出的粒子在磁场中运动的最短时间等于$\frac{1}{6}$T,知对应的圆心角为60°,则对应弦长最短,根据几何关系求出圆周运动的半径;当对应的圆弧弦长为直径时,射出点距离O点最远,根据几何关系求出粒子运动轨迹和0C边界的交点到0点的最远距离.当对应的圆弧弦长为直径时,对应的圆心角最大,对应的时间最长.
解答 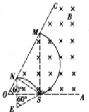 解:AB、粒子在磁场中做圆周运动的半径r=$\frac{mv}{qB}$均相同,周期T=$\frac{2πm}{qB}$也均相同.
解:AB、粒子在磁场中做圆周运动的半径r=$\frac{mv}{qB}$均相同,周期T=$\frac{2πm}{qB}$也均相同.
如图所示,设粒子从边界OC上的N点射出时运动时间最短,则对应弦长最短,故SN⊥OC,且SN的对应的圆心角为60°,则粒子做圆周运动的半径r=$\frac{\sqrt{3}}{2}$L.
设M点为距O的最远射出点,则SM为直径,则∠SMN=30°,所以OM=2L.因为粒子圆周运动轨迹的直径大于L,所以粒子一定能过O点.故A、B正确.
CD、粒子在磁场中的最大弦长等于直径,所以对应的最长时间为$\frac{1}{2}$T,而最小时间为$\frac{T}{6}$.故C正确,D错误.
本题选错误的,故选:D
点评 本题考查带电粒子在磁场中的运动,关键是明确在轨道半径一定的情况下,对数学几何能力的要求较高,需加强训练.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
6.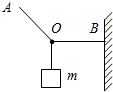 如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
 如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 最大值是mg | D. | 最小值是mg |
7.哪位科学家证明了天电与摩擦产生的电是相同的( )
| A. | 焦耳 | B. | 库伦 | C. | 莱顿 | D. | 富兰克林 |
11.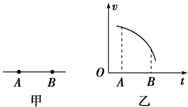 如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
 如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )| A. | 该电场是匀强电场 | |
| B. | A、B两点的电势相比一定是φA<φB | |
| C. | A、B两点的场强大小相比一定是EA<EB | |
| D. | 该电荷在两点的电势能大小相比一定是EpA<EpB |
8.下列图象属于匀变速直线运动的是( )
| A. |  | B. | 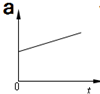 | C. | 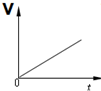 | D. |  |
5.张明同学测得一小球从一高楼顶自由下落到地面所用的时间为3s,取g=10m/s2,则下列说法正确的是( )
| A. | 小球从开始下落到着地过程的平均速度大小为30m/s | |
| B. | 该楼的高度为90m | |
| C. | 小球从开始下落到一半高度处所用时间为1.5s | |
| D. | 小球在最后1s内的位移大小为25m |
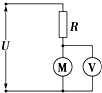 如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=0.8Ω,电路中另一电阻R=8Ω,直流电压U=160V,理想电压表示数UV=120V.试求:
如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=0.8Ω,电路中另一电阻R=8Ω,直流电压U=160V,理想电压表示数UV=120V.试求: