题目内容
(2005?广州模拟)有一同学测量小车从斜面上下滑所受到的阻力大小,他利用一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图甲所示.图乙是打出的纸带的一段,已量出各相邻计数段的长度分别为:S1、S2、S3、S4、S5、S6、S7、S8.
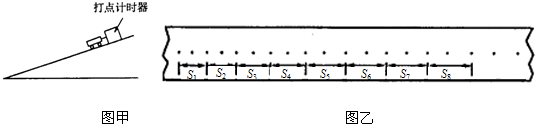
(1)已知打点计时器使用的交流电频率f=50Hz,打点的周期为
.
(2)为了求出小车在下滑过程中所受的阻力,还需测量的物理量有
(3)用加速度a及其他需要测得的量表示阻力的计算式为f=

(1)已知打点计时器使用的交流电频率f=50Hz,打点的周期为
0.02
0.02
s.用以上已知的物理量表示小车下滑的加速度算式为a=| f2[(s5+s6+s7+s8)-(s1+s2+s3+s4)] |
| 64 |
| f2[(s5+s6+s7+s8)-(s1+s2+s3+s4)] |
| 64 |
(2)为了求出小车在下滑过程中所受的阻力,还需测量的物理量有
小车质量m,斜面上任意两点间距离l及这两点的高度差h
小车质量m,斜面上任意两点间距离l及这两点的高度差h
.(3)用加速度a及其他需要测得的量表示阻力的计算式为f=
mg
-ma
| h |
| l |
mg
-ma
.| h |
| l |
分析:解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项.
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的加速度.
为了求出小车在下滑过程中所受的阻力,我们应该想到运用牛顿第二定律去求解.
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的加速度.
为了求出小车在下滑过程中所受的阻力,我们应该想到运用牛顿第二定律去求解.
解答:解:(1)已知打点计时器使用的交流电频率f=50Hz,打点的周期为0.02s,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x5-x1=4a1T2
x6-x2=4a2T2
x7-x3=4a3T2
x8-x4=4a4T2
T=
为了更加准确的求解加速度,我们对四个加速度取平均值
得:a=
(a1+a2+a3+a4)
解得:a=
(2)小车在下滑过程受重力、支持力、摩擦阻力.设斜面倾角为θ
将重力分解,由牛顿第二定律得:
mgsinθ-f=ma
f=mgsinθ-ma
为了求出小车在下滑过程中所受的阻力,那么我们需要测量小车质量,倾角直接测量很困难.我们可以测出斜面上任意两点间的距离l及这两点的高度差h,
通过
=sinθ代替.
(3)所以得:f=mg
-ma
故答案为:(1)0.02;
,
(2)小车质量m; 斜面上任意两点间距离l及这两点的高度差h (3)mg
-ma
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x5-x1=4a1T2
x6-x2=4a2T2
x7-x3=4a3T2
x8-x4=4a4T2
T=
| 2 |
| f |
为了更加准确的求解加速度,我们对四个加速度取平均值
得:a=
| 1 |
| 4 |
解得:a=
| f2[(s5+s6+s7+s8)-(s1+s2+s3+s4)] |
| 64 |
(2)小车在下滑过程受重力、支持力、摩擦阻力.设斜面倾角为θ
将重力分解,由牛顿第二定律得:
mgsinθ-f=ma
f=mgsinθ-ma
为了求出小车在下滑过程中所受的阻力,那么我们需要测量小车质量,倾角直接测量很困难.我们可以测出斜面上任意两点间的距离l及这两点的高度差h,
通过
| h |
| l |
(3)所以得:f=mg
| h |
| l |
故答案为:(1)0.02;
| f2[(s5+s6+s7+s8)-(s1+s2+s3+s4)] |
| 64 |
(2)小车质量m; 斜面上任意两点间距离l及这两点的高度差h (3)mg
| h |
| l |
点评:能够运用逐差法求解加速度.
能够把纸带的问题结合动力学知识运用解决问题.
能够把纸带的问题结合动力学知识运用解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
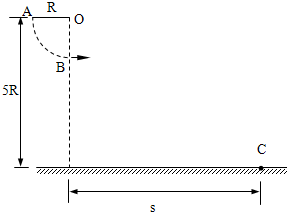 (2005?广州模拟)如图所示,一对杂技演员(都视为质点)乘秋千(秋千绳处于水平位置)从A点由静止出发绕O点下摆,当摆到最低点B时,女演员在极短时间内将男演员沿水平方向推出,然后自已刚好能回到高处A.求男演员落地点C 与O 点的水平距离s.已知男演员质量m1,和女演员质量m2之比
(2005?广州模拟)如图所示,一对杂技演员(都视为质点)乘秋千(秋千绳处于水平位置)从A点由静止出发绕O点下摆,当摆到最低点B时,女演员在极短时间内将男演员沿水平方向推出,然后自已刚好能回到高处A.求男演员落地点C 与O 点的水平距离s.已知男演员质量m1,和女演员质量m2之比 (2005?广州模拟)图所示,a、b、c为电场中同一条水平方向电场线上的三点,c为ab中点.a、b电势分别为Ua=5V、Ub=3V.下列叙述正确的是( )
(2005?广州模拟)图所示,a、b、c为电场中同一条水平方向电场线上的三点,c为ab中点.a、b电势分别为Ua=5V、Ub=3V.下列叙述正确的是( )