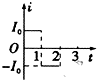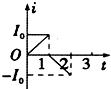题目内容
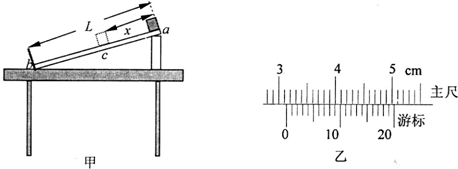
1.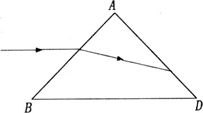 如图,一个三棱镜的截面为等腰直角△ABD,∠A为直角.此截面所在平面内的光线沿平行于BD边的方向射到AB边,进入棱镜后直接射到AD边上,并刚好能发生全反射.真空中光速为c.求光在该棱镜材料中传播的速度.
如图,一个三棱镜的截面为等腰直角△ABD,∠A为直角.此截面所在平面内的光线沿平行于BD边的方向射到AB边,进入棱镜后直接射到AD边上,并刚好能发生全反射.真空中光速为c.求光在该棱镜材料中传播的速度.
分析 由题意画出光路图,由几何关系分析出各角的大小,则由折射定律及全反射可得出临界角与折射率的关系,联立可求得折射率,由v=$\frac{c}{n}$求解光在该棱镜材料中传播的速度.
解答  解:光射到AB面时的入射角 θ1=45°
解:光射到AB面时的入射角 θ1=45°
设棱镜的折射率为n,根据折射定律有 n=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$ ①
折射光线在AD面发生全反射,则 sinC=$\frac{1}{n}$ ②
根据几何关系有 θ2+C=90° ③
联立解得 n=$\sqrt{\frac{3}{2}}$ ④
则光在该棱镜材料中传播的速度为 v=$\frac{c}{n}$=$\frac{\sqrt{6}}{3}$c ⑤
答:光在该棱镜材料中传播的速度为$\frac{\sqrt{6}}{3}$c.
点评 解答本题的关键在于利用几何关系找出入射角、折射角和它们之间的关系,由折射定律可列出方程求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.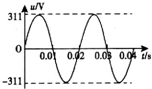 如图为理想变压器原线圈所接交流电压的波形.原、副线圈匝数比n1:n2=10:1,串联在副线圈电路中电流表的示数为10A,下列说法正确的是( )
如图为理想变压器原线圈所接交流电压的波形.原、副线圈匝数比n1:n2=10:1,串联在副线圈电路中电流表的示数为10A,下列说法正确的是( )
 如图为理想变压器原线圈所接交流电压的波形.原、副线圈匝数比n1:n2=10:1,串联在副线圈电路中电流表的示数为10A,下列说法正确的是( )
如图为理想变压器原线圈所接交流电压的波形.原、副线圈匝数比n1:n2=10:1,串联在副线圈电路中电流表的示数为10A,下列说法正确的是( )| A. | 变压器原线圈中的电流为1A | B. | 变压器的输出功率为311W | ||
| C. | 变压器输出端电压最大值为31.1V | D. | 变压器输出端交流电的频率为50Hz |
13.在进行飞镖训练时,打飞镖的靶上共标有10环,且第10环的半径最小,为1cm,第9环的半径为2 cm,…,以此类推,若靶的半径为10cm,当人离靶的距离为5m,将飞镖对准10环中心以水平速度v投出,g=10m/s2.则下列说法中,不正确的是( )
| A. | 当v≥50 m/s时,飞镖将射中第8环线以内 | |
| B. | 当v≥50 m/s时,飞镖将射中第6环线内 | |
| C. | 若要击中第10环的圆内,飞镖的速度v至少应为50$\sqrt{5}$ m/s | |
| D. | 若要击中靶子,飞镖的速度v至少应为25$\sqrt{2}$ m/s |
2. 如图所示,两根足够长的水平平行金属导轨相距为L,固定在水平桌面上,导轨右端连接电动势为E(内阻不计)的电池及电阻R.长度略大于L的金属棒垂直于导轨放置,若在整个空间加上方向竖直向下的匀强磁场,闭合开关后金属棒由静止开始滑动一段时间后可达到匀速状态,且不同大小的磁感应强度,达到匀速状态的速度不同.设运动时金属棒与导轨间的摩擦力恒为f.不考虑金属棒中电流的磁场及金属棒的电阻.下列说法正确的是( )
如图所示,两根足够长的水平平行金属导轨相距为L,固定在水平桌面上,导轨右端连接电动势为E(内阻不计)的电池及电阻R.长度略大于L的金属棒垂直于导轨放置,若在整个空间加上方向竖直向下的匀强磁场,闭合开关后金属棒由静止开始滑动一段时间后可达到匀速状态,且不同大小的磁感应强度,达到匀速状态的速度不同.设运动时金属棒与导轨间的摩擦力恒为f.不考虑金属棒中电流的磁场及金属棒的电阻.下列说法正确的是( )
 如图所示,两根足够长的水平平行金属导轨相距为L,固定在水平桌面上,导轨右端连接电动势为E(内阻不计)的电池及电阻R.长度略大于L的金属棒垂直于导轨放置,若在整个空间加上方向竖直向下的匀强磁场,闭合开关后金属棒由静止开始滑动一段时间后可达到匀速状态,且不同大小的磁感应强度,达到匀速状态的速度不同.设运动时金属棒与导轨间的摩擦力恒为f.不考虑金属棒中电流的磁场及金属棒的电阻.下列说法正确的是( )
如图所示,两根足够长的水平平行金属导轨相距为L,固定在水平桌面上,导轨右端连接电动势为E(内阻不计)的电池及电阻R.长度略大于L的金属棒垂直于导轨放置,若在整个空间加上方向竖直向下的匀强磁场,闭合开关后金属棒由静止开始滑动一段时间后可达到匀速状态,且不同大小的磁感应强度,达到匀速状态的速度不同.设运动时金属棒与导轨间的摩擦力恒为f.不考虑金属棒中电流的磁场及金属棒的电阻.下列说法正确的是( )| A. | 当磁感应强度B=$\frac{2fR}{LE}$时,金属棒达到匀速状态的速度具有最大值 | |
| B. | 金属棒达到匀速状态的速度具有最大值时,其两端电压为$\frac{E}{3}$ | |
| C. | 金属棒达到匀速状态的速度具有最大值时,通过的电流为$\frac{E}{2R}$ | |
| D. | 金属棒达到匀速状态的速度具有最大值时,其克服摩擦力的功率为$\frac{{E}^{2}}{4R}$ |
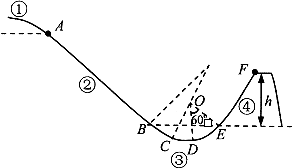 自由式滑雪空中技巧是一项有极大观赏性的运动,其场地由①出发区、②助滑坡、③过渡区、④高度h=4m的跳台组成.其中过渡区的CDE部分是半径为R=4m圆弧,D是最低点,∠DOE=60°,如图所示.比赛时运动员由A点静止出发进入助滑区,经过渡区后,沿跳台的斜坡匀减速上滑,至跳台的F处飞出表演空中动作.运动员要成功完成空中动作,必须在助滑区用滑雪杆助滑,使离开F点时速度在36km/h到48km/h之间.不计所有阻力,已知$\overline{AB}=2\overline{EF}$,取g=10m/s2.
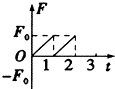
自由式滑雪空中技巧是一项有极大观赏性的运动,其场地由①出发区、②助滑坡、③过渡区、④高度h=4m的跳台组成.其中过渡区的CDE部分是半径为R=4m圆弧,D是最低点,∠DOE=60°,如图所示.比赛时运动员由A点静止出发进入助滑区,经过渡区后,沿跳台的斜坡匀减速上滑,至跳台的F处飞出表演空中动作.运动员要成功完成空中动作,必须在助滑区用滑雪杆助滑,使离开F点时速度在36km/h到48km/h之间.不计所有阻力,已知$\overline{AB}=2\overline{EF}$,取g=10m/s2.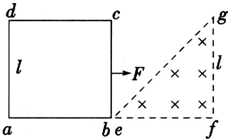 在光滑水平桌面上有一边长为l的正方形线框abcd,bc边右侧有一等腰直角三角形匀强磁场区域efg,三角形腰长为l,磁感应强度竖直向下,a、b、e、f在同一直线上,其俯视图如图所示,线框从图示位置在水平拉力F作用下以速度v向右匀速穿过磁场区,线框中感应电流i-t和F-t图象正确的是(以逆时针方向为电流的正方向,以水平向右的拉力为正,时间单位为$\frac{l}{t}$)( )
在光滑水平桌面上有一边长为l的正方形线框abcd,bc边右侧有一等腰直角三角形匀强磁场区域efg,三角形腰长为l,磁感应强度竖直向下,a、b、e、f在同一直线上,其俯视图如图所示,线框从图示位置在水平拉力F作用下以速度v向右匀速穿过磁场区,线框中感应电流i-t和F-t图象正确的是(以逆时针方向为电流的正方向,以水平向右的拉力为正,时间单位为$\frac{l}{t}$)( )