题目内容
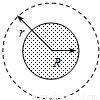
设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱围绕火星做圆周运动的轨道舱.为了安全,返回舱与轨道舱对接时,二者必须具有相同的速度.返回舱在返回过程中需克服火星引力做功W=mgR(1- ),式中各量分别为:返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r,如图所示.不计火星表面大气对返回舱的阻力和火星自转的影响.求:
),式中各量分别为:返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r,如图所示.不计火星表面大气对返回舱的阻力和火星自转的影响.求:(1)返回舱与轨道舱对接时,返回舱的动能;
(2)该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?
【答案】分析:根据火星表面的重力等于万有引力列出等式.
研究轨道舱绕卫星做匀速圆周运动,根据万有引力提供向心力,列出等式求解宇航员乘坐返回舱与轨道舱对接时速度.
根据能量守恒求解返回轨道舱至少需要获得的能量.
解答:解:(1)设火星的质量为M,轨道舱的质量为m1.在火星表面处有
轨道舱绕火星做圆周运动时,应有
对接时,返回舱与轨道舱的速度相等.由以上两式解得
所以对接时返回舱的动能为
(2)设返回舱返回过程中需要的能量为E,由能量守恒定律知,E-W=Ek,
∵返回舱返回过程克服引力做功W=mgR(1- )
)
∴
答:(1)返回舱与轨道舱对接时,返回舱的动能为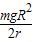 ;
;
(2)该宇航员乘坐的返回舱至少需要获得 的能量,才能返回轨道舱.
的能量,才能返回轨道舱.
点评:向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.忽略星球自转的影响,能根据万有引力等于重力列出等式.
研究轨道舱绕卫星做匀速圆周运动,根据万有引力提供向心力,列出等式求解宇航员乘坐返回舱与轨道舱对接时速度.
根据能量守恒求解返回轨道舱至少需要获得的能量.
解答:解:(1)设火星的质量为M,轨道舱的质量为m1.在火星表面处有

轨道舱绕火星做圆周运动时,应有

对接时,返回舱与轨道舱的速度相等.由以上两式解得

所以对接时返回舱的动能为

(2)设返回舱返回过程中需要的能量为E,由能量守恒定律知,E-W=Ek,
∵返回舱返回过程克服引力做功W=mgR(1-
 )
)∴

答:(1)返回舱与轨道舱对接时,返回舱的动能为
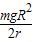 ;
;(2)该宇航员乘坐的返回舱至少需要获得
 的能量,才能返回轨道舱.
的能量,才能返回轨道舱.点评:向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.忽略星球自转的影响,能根据万有引力等于重力列出等式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2006?永州模拟)设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.已知返回舱返回过程中需克服火星的引力做功
(2006?永州模拟)设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.已知返回舱返回过程中需克服火星的引力做功 设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.已知返回舱返回过程中需克服火星的引力做功
设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.已知返回舱返回过程中需克服火星的引力做功 设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.求该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?
设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.求该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?