题目内容
（2006?静安区模拟）如图所示ABC是一块三角形的均匀大木板，已知AB＜AC＜BC．现在有甲、乙、丙三个人来抬木板，甲抬A角，乙抬B角，丙抬C角，则抬起来后，每个人所用力的大小关系是（ ）分析：以三角形的一个边为杠杆转动的支点，根据杠杆平衡条件分别求出甲、乙、丙三个人抬木板所用的力与均匀大木板的重力之间的关系，然后比较其大小．
解答：解：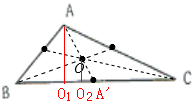
如图，O为三角形的重心（各边中线交点），木板受到向上的力FA、FB、FC，向下的重力G，木板水平平衡，
先以三角形木板BC边为轴，则三角形在A的抬力F甲和三角形木板重力G作用下，处于平衡状态，力臂为A01、OO2，
则：F甲×A01=G×OO2，
由三角形的中线、重心的几何知识得：A01=3?OO2，
∴F甲=
G，
同理可得：F乙=
G，F丙=
G，
∴F甲=F乙=F丙
故选C．
如图，O为三角形的重心（各边中线交点），木板受到向上的力FA、FB、FC，向下的重力G，木板水平平衡，先以三角形木板BC边为轴，则三角形在A的抬力F甲和三角形木板重力G作用下，处于平衡状态，力臂为A01、OO2，
则：F甲×A01=G×OO2，
由三角形的中线、重心的几何知识得：A01=3?OO2，
∴F甲=
| 1 |
| 3 |
同理可得：F乙=
| 1 |
| 3 |
| 1 |
| 3 |
∴F甲=F乙=F丙
故选C．
点评：本题的解答过程应从另一各角度分析，关键是将三角形的一个边为转动的支点，这样能简化解答分析过程，便于理解，这类似于关门的杠杆平衡．难点是力臂的确定和在AO1A′的三角形中利用的几何知识判断出A01=3?OO2．
练习册系列答案
相关题目
（2006?静安区模拟）如右图所示，倾角为θ=30°的直角三角形底边长为2L，处于水平位置，斜面绝缘光滑，在底边中点O处固定一正点电荷Q．让一质量为m的带正电的点电荷q，从斜面顶端A处释放，沿斜面下滑（不脱离斜面）．现测得它滑到B点在斜边上的垂足D点处的速度为v，加速度为a，方向沿斜面向下．则q滑到斜面底端C点时的速度为
（2006?静安区模拟）如右图所示，劈a放在光滑水平桌面上，把b物体放在光滑斜面的顶端，b由静止开始沿斜面自由滑下的过程中，a对b的弹力对b做的功为W1，b对a的弹力对a做的功为w2，则下列关系正确的是（ ）