题目内容
11.将质量为0.5kg的小球,以30m/s的速度竖直上抛,经过2.5s小球到达最高点(取g=10m/s),求;(1)小球在上升过程中受到的空气的平均阻力;
(2)小球在最高点时的加速度大小;
(3)若空气阻力不变,小球下落时的加速度为多大?
分析 (1)根据匀变速直线运动的速度时间公式求出小球上升过程中的加速度大小,结合牛顿第二定律求出上升过程中的空气的平均阻力.
(2)由于空气阻力与速度有关,所以在最高点速度为零,阻力为零,结合牛顿第二定律求出小球在最高点的加速度大小.
(3)根据牛顿第二定律求出小球下落时的加速度大小.
解答 解:(1)根据速度时间公式得,小球上升过程中的加速度大小为:a=$\frac{{v}_{0}}{t}=\frac{30}{2.5}m/{s}^{2}=12m/{s}^{2}$,
根据牛顿第二定律得:mg+f=ma,
解得:f=ma-mg=0.5×(12-10)N=1N.
(2)在最高点,速度为零,则阻力为零,根据牛顿第二定律得,加速度为:$a′=\frac{mg}{m}=g=10m/{s}^{2}$.
(3)下落过程中的加速度为:$a″=\frac{mg-f}{m}=\frac{0.5×10-1}{0.5}m/{s}^{2}=8m/{s}^{2}$.
答:(1)小球在上升过程中受到的空气的平均阻力为1N;
(2)小球在最高点时的加速度大小为10m/s2;
(3)若空气阻力不变,小球下落时的加速度为8m/s2.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,注意上升和下降过程中空气阻力方向不同.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.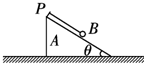 如图所示,质量为M、倾角为θ的楔形滑块A置于水平面上,细线的一端固定于滑块的顶端P处,细线另一端栓一质量为m的小球B.各接触面均光滑,现对滑块施加某一方向的恒力F,要使小球B能相对斜面静止.下列说法正确的是( )
如图所示,质量为M、倾角为θ的楔形滑块A置于水平面上,细线的一端固定于滑块的顶端P处,细线另一端栓一质量为m的小球B.各接触面均光滑,现对滑块施加某一方向的恒力F,要使小球B能相对斜面静止.下列说法正确的是( )
 如图所示,质量为M、倾角为θ的楔形滑块A置于水平面上,细线的一端固定于滑块的顶端P处,细线另一端栓一质量为m的小球B.各接触面均光滑,现对滑块施加某一方向的恒力F,要使小球B能相对斜面静止.下列说法正确的是( )
如图所示,质量为M、倾角为θ的楔形滑块A置于水平面上,细线的一端固定于滑块的顶端P处,细线另一端栓一质量为m的小球B.各接触面均光滑,现对滑块施加某一方向的恒力F,要使小球B能相对斜面静止.下列说法正确的是( )| A. | 无论恒力F多大,只要恒力F水平向右就行 | |
| B. | 恒力F水平向左时,临界条件是A、B之间刚好无弹力 | |
| C. | 恒力F水平向右时,小球保持相对静止的条件是F≤(M+m)gtan θ | |
| D. | 恒力F水平向右时,满足F≤(M+m)gcot θ |
19.在体育测试中,老师用频闪相机拍摄了同学立定跳远时起跳、腾空、落地的照片(如图甲),简化图如图乙所示.请你根据体育常识估算该同学起跳瞬间消耗的能量最接近( )


| A. | 8000J | B. | 600J | C. | 60J | D. | 6000J |
20.云南彝良发生地震后,在前往救灾路上,一辆救灾汽车由静止开始做匀变速直线运动,刚运动了8s,由于前方突然有巨石滚在路中央,所以又紧急刹车,经4s停在巨石前.汽车在加速、减速运动中说法正确的是( )
| A. | 加速度之比a1:a2=2:1 | B. | 平均速度之比v1:v2=2:1 | ||
| C. | 位移之比x1:x2=2:1 | D. | 加速度之比a1:a2=1:2 |
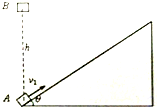 如图所示,在水平地面上固定一倾角θ=30°的长斜面体,物体A以v1的初速度沿斜面上滑,同时在物体A的正上方h=1.25m处一物体B自由下落,当物体A回到出发点时恰好被B物体击中.已知物体A与斜面体间的动摩擦因数为μ=$\frac{\sqrt{3}}{5}$.(A、B均可看作质点.g取10m∕s2)求:
如图所示,在水平地面上固定一倾角θ=30°的长斜面体,物体A以v1的初速度沿斜面上滑,同时在物体A的正上方h=1.25m处一物体B自由下落,当物体A回到出发点时恰好被B物体击中.已知物体A与斜面体间的动摩擦因数为μ=$\frac{\sqrt{3}}{5}$.(A、B均可看作质点.g取10m∕s2)求: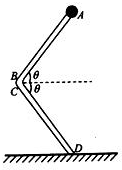 如图所示,竖直面内有一“<”形杆ABCD,杆的D端固定在水平地面上,杆的AB部分光滑,CD部分粗糙.两部分与水平面间的夹角均为θ,长度均为L.BC是一段很小的光滑圆弧,圆弧的两端分别与AB和CD相切.质量为m的小球中间有孔,穿在杆上并由静止开始从A端下滑,已知小球到达D点时速度大小为v,若不考虑小圆弧BC的长度和小球在小圆弧上的运动时间,重力加速的大小为g,求:
如图所示,竖直面内有一“<”形杆ABCD,杆的D端固定在水平地面上,杆的AB部分光滑,CD部分粗糙.两部分与水平面间的夹角均为θ,长度均为L.BC是一段很小的光滑圆弧,圆弧的两端分别与AB和CD相切.质量为m的小球中间有孔,穿在杆上并由静止开始从A端下滑,已知小球到达D点时速度大小为v,若不考虑小圆弧BC的长度和小球在小圆弧上的运动时间,重力加速的大小为g,求: 如图所示,半径为R=0.1m的光滑圆形轨道BCD与水平轨道AB在B点平滑连接,质量为m=100g的小物块静止放置在A点,A、B距离为1.3m,已知小物块与水平面间的动摩擦因数为μ=0.5,现对小物块施加水平向右的力F,F=1N,作用一段时间后撤去F,小物块刚好能通过光滑圆形轨道的最高点D,g取10m/s2,求:
如图所示,半径为R=0.1m的光滑圆形轨道BCD与水平轨道AB在B点平滑连接,质量为m=100g的小物块静止放置在A点,A、B距离为1.3m,已知小物块与水平面间的动摩擦因数为μ=0.5,现对小物块施加水平向右的力F,F=1N,作用一段时间后撤去F,小物块刚好能通过光滑圆形轨道的最高点D,g取10m/s2,求: