题目内容
（2010?桂林二模）如图所示，水平面上放有质量均为m=1kg的物块A和B，A、B与地面的动摩擦因数分别为μ1=0.4和μ2=0.1，相距l=0.75m．现给物块A一初速度使之向B运动，与此同时给物块B一个F=3N水平向右的力由静止开始运动，经过一段时间A恰好能追上B．g=10m/s2．求：（1）物块B运动的加速度大小；
（2）物块A初速度大小．
分析：（1）物块B在水平方向受到拉力F和摩擦力，根据牛顿第二定律求解物块B的加速度大小．
（2）根据牛顿第二定律求出A的加速度．由题，A恰好能追上B，相遇时，两者的速度相等，位移之差等于l，由位移公式和速度公式，结合关系式求出物块A初速度大小．
（2）根据牛顿第二定律求出A的加速度．由题，A恰好能追上B，相遇时，两者的速度相等，位移之差等于l，由位移公式和速度公式，结合关系式求出物块A初速度大小．
解答：解：（1）对B，根据牛顿第二定律得：F-μ2mg=maB
求得：aB=2m/s2．
（2）设A经过t时间追上B，对A，由牛顿第二定律得：
μ1mg=maA
sA=v0t-
aAt2
sB=
aBt2
恰好追上的条件为：
v0-aAt=aBt
sA-sB=l
代入数据解得：v0=3m/s
答：
（1）物块B运动的加速度大小是2m/s2；
（2）物块A初速度大小是3m/s．
求得：aB=2m/s2．
（2）设A经过t时间追上B，对A，由牛顿第二定律得：
μ1mg=maA
sA=v0t-
| 1 |
| 2 |
sB=
| 1 |
| 2 |
恰好追上的条件为：
v0-aAt=aBt
sA-sB=l
代入数据解得：v0=3m/s
答：
（1）物块B运动的加速度大小是2m/s2；
（2）物块A初速度大小是3m/s．
点评：本题是匀减速运动追及匀加速运动的类型，关键要抓住两个物体的关系．
练习册系列答案
相关题目
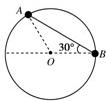（2010?桂林二模）如图所示，竖直面内的固定圆环光滑，两个有孔的小球A和B套在环上．中间用一根轻绳相连，B处在过圆心的水平线上，绳与水平方向的夹角为30°时A、B均保持静止，已知B的质量为m，下列判断正确的是（ ）