��Ŀ����
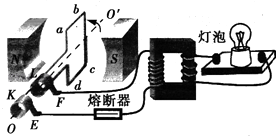
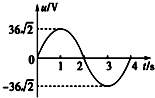
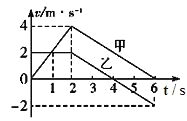
����Ŀ����ͼ��a����ʾ�����Ϊl�����費�ƵĹ⻬����̶������Ϊ�ȵ�б���ϣ�����������з���ֱ��б�����ǿ�ų����Ÿ�Ӧǿ�Ⱥ�ΪB���䣻����������д�ֱ��б�����µ���ǿ�ų�����Ÿ�Ӧǿ��Bt�Ĵ�С��ʱ��仯�Ĺ�����ͼ��b����ʾ��t=0ʱ���ڹ���϶˵Ľ���ϸ��ab����ͼλ���ɾ�ֹ��ʼ�ص����»���ͬʱ�¶˵���һ����ϸ��cd��λ��������ڵĵ������ɾ�ֹ�ͷţ���ab���˶����������±߽�EF��֮ǰ��cd��ʼ�վ�ֹ�������������뵼��Ӵ����ã���֪cd��������Ϊm������ΪR��ab������������ֵ��δ֪���������б��ij���Ϊ2l����t=txʱ�̣�txδ֪��ab��ǡ����������������ٶ�Ϊg����
��1��ͨ��cd�������ķ����������ڴų��ķ���
��2����ab������������˶�ʱcd�����ĵĵ繦�ʣ�
��3��ab����ʼ�»���λ����EF�ľ��룻
��4��ab���ӿ�ʼ�»���EF�Ĺ����У���·�в����ܵ��������������B��l���ȡ�m��R��g��ʾ��
���𰸡�
��1���⣺ͨ��cd���ĵ������� d��c
����I�ڴų�����Ϊ��ֱ��б������
��ͨ��cd�������ķ���d��c��������ڴų��ķ���ֱ��б�����ϣ�
��2���⣺cd��ƽ�⣬
BIl=mgsin�ȣ�
I= ![]()
��������d��c��
��ab��������II���˶�ʱcd�����ĵĵ繦�� ![]()
�𣺵�ab������������˶�ʱcd�����ĵĵ繦�� ![]() ��
��
��3���⣺ǰ�����·��Ӧ�綯�Ʋ��䣬
![]() =Blvx��
=Blvx��
�� ![]() =Blvx��
=Blvx��
���l=vxtx
ab�����������֮ǰ���ܴų��������ã����ȼ���ֱ���˶���
S1= ![]() ��0+v��tx=0.5l
��0+v��tx=0.5l
��ab����ʼ�»���λ����EF�ľ���0.5l��
��4���⣺ab������������������ֱ���˶���
t2=tx��
��ʱ��t��=tx+t2=2tx��
�綯��E=Blvx���䣬
��������Q=EIt��=2mgvxtxsin��=2mglsin��
��ab���ӿ�ʼ�»���EF�Ĺ����У���·�в����ܵ�����2mglsin��
����������1���������ֶ����жϳ�ab���еĵ������Ӷ��ó�ͨ��cd���еĵ���������cd�����ھ�ֹ������ƽ����������������ķ��������ֶ����жϳ�����I�ڴų��ķ���
��2����cd��������ƽ�������Ӧ�����Ĵ�С������P=I2R�����ab��������II���˶�ʱcd�����ĵĵ繦�ʣ�
��3����ab����II����ǰ���·�еĵ綯�Ʋ��䣬���ų��仯�����綯���뵼���и�Ÿ��߲����綯����ȣ��ݴ�������������IIʱ�ٶȴ�С��Ȼ����ݵ�����ȼ����»����ص㼴����������
��4����·�е����㶨������Q=EIt����������
�����㾫����������Ĺؼ����������Ÿ�Ӧ���·�����֪ʶ�������÷����ڵ�Ÿ�Ӧ���ɺ���ζ���ȷ����Ӧ�綯�ƵĴ�С�ͷ�����Ч��·������ȫ��·ŷķ���ɣ���������·���ʣ��繦�ʵȹ�ʽ������⣬�Լ��Ե�Ÿ�Ӧ����ѧ�����⣬�˽��÷����ڵ�Ÿ�Ӧ���ɺ���ζ������Ӧ�綯�ƵĴ�С�ͷ������·�е���ǿ�ȣ������о�������������������������������ֶ���ȷ���䷽���ж���ѧ���̻�ƽ�ⷽ����⣮