题目内容
4.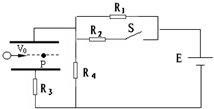 如图所示,水平放置的平行板电容器,两板间距为d=8cm,板长为L=25cm,电源电动势为E=6V、r=1Ω,R1=R2=R3=2Ω,R4=3Ω.有一带电液滴以v0=0.5m/s的初速度从板间的正中点水平射入,电键S断开时恰好做匀速直线运动,当它运动到P处时迅速将电键S闭合,液滴刚好从金属板末端飞出,求:
如图所示,水平放置的平行板电容器,两板间距为d=8cm,板长为L=25cm,电源电动势为E=6V、r=1Ω,R1=R2=R3=2Ω,R4=3Ω.有一带电液滴以v0=0.5m/s的初速度从板间的正中点水平射入,电键S断开时恰好做匀速直线运动,当它运动到P处时迅速将电键S闭合,液滴刚好从金属板末端飞出,求:(1)电键S闭合后液滴经过P点以后的加速度(g取10m/s2)
(2)液滴从射入开始匀速运动到P点所用时间.
分析 (1)根据电路规律可得出电容器两端的电压,再对小球分析可求得小球的电性及电量;分析开关断开后电路结构的变化,再根据电容器两端电压的变化分析电场力的变化,从而求出加速度.
(2)开始时液滴做匀速直线运动,后来做类平抛运动,结合两种运动的特点,即可求出.
解答 解:(1)开始时R1与R4串联;电容器两端的电压与R4两端的电压相等,电路中的电流:
${I}_{1}=\frac{E}{r+{R}_{1}+{R}_{4}}=\frac{6}{1+2+3}=1$A
R4两端的电压:U=I1R4=1×3=3V
电键闭合,R1与R2并联后与R4串联;电容器两端的电压与R4两端的电压相等.${R}_{并}=\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}=\frac{2×2}{2+2}=1$Ω
开始时的电流:${I}_{2}=\frac{E}{r+{R}_{并}+{R}_{4}}=\frac{6}{1+1+3}=1.2$A
R4两端的电压:U′=I2R4=1.2×3=3.6V
开始时液滴做匀速直线运动,得:mg=q$\frac{U}{d}$
电键闭合后,极板之间的电势差增大,所以电场强度增大,电场力大于重力,液滴向上做加速运动,满足:$q\frac{U′}{d}-mg=ma$
联立得:$a=\frac{1}{5}g=\frac{1}{5}×10=2m/{s}^{2}$
(2)由题,液滴刚好从金属板末端飞出,则偏转的距离:y=$\frac{1}{2}$d
由$y=\frac{1}{2}a{t}_{2}^{2}$
联立得:${t}_{2}=\sqrt{\frac{d}{a}}=\sqrt{\frac{0.08}{2}}=0.2$s
液滴穿过电场的时间:$t=\frac{L}{{v}_{0}}=\frac{0.25}{0.5}=0.5$s
所以:液滴从射入开始匀速运动到P点所用时间:t1=t-t2=0.5-0.2=0.3s
答:(1)电键S闭合后液滴经过P点以后的加速度是2m/s2;
(2)液滴从射入开始匀速运动到P点所用时间是0.3s.
点评 本题为闭合电路欧姆定律中的含容电路与带电粒子在电场中的运动的结合,要注意正确分析电路结构,明确电阻R3作为导线处理.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
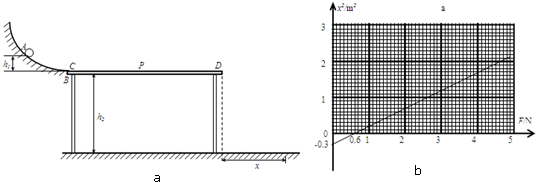
计算高手系列答案 如图所示,光滑轨道ABCD是过山车轨道的模型,最低点B处的入、出口靠近但相互错开,C是半径为R的圆形轨道的最高点,BD部分水平,末端D点与右端足够长的水平粗糙传送带无缝连接,传送带以恒定速度v逆时针转动,现将一质量为m的小滑块从轨道AB上某一固定位置A由静止释放,滑块能通过C点后再经D点滑上传送带,则( )
如图所示,光滑轨道ABCD是过山车轨道的模型,最低点B处的入、出口靠近但相互错开,C是半径为R的圆形轨道的最高点,BD部分水平,末端D点与右端足够长的水平粗糙传送带无缝连接,传送带以恒定速度v逆时针转动,现将一质量为m的小滑块从轨道AB上某一固定位置A由静止释放,滑块能通过C点后再经D点滑上传送带,则( )| A. | 固定位置A到B点的竖直高度可能为2R | |
| B. | 滑块在传送带上向右运动的最大距离与传送带速度v有关 | |
| C. | 滑块可能重新回到出发点A处 | |
| D. | 无论传送带速度v多大,滑块与传送带摩擦产生的热量都一样多 |
| A. | 因甲队胜而乙队负,所以甲队拉绳子的力大于乙队拉绳子的力 | |
| B. | 只有在两队相持不动时,两队拉力才大小相等 | |
| C. | 只有在甲队拉动乙队时,甲队拉力才大于乙队 | |
| D. | 甲队获胜的原因是甲队受到地面的最大静摩擦力大于乙队受到地面的最大静摩擦力 |

| A. | 甲乙运动的速度方向相反 | B. | 甲起动的时间比乙早t1秒 | ||
| C. | 当t=t2时两物体相距最远 | D. | 当t=t3时两物体相距S0米 |

 如图所示,一质量为m、带电荷量为+q的粒子,速度大小为v0、方向沿y轴正方向,从O点射入圆形匀强磁场区域.磁场的感应强度为B,磁场方向垂直纸面向外.粒子飞出磁场区域后,从b处穿过x轴,在b点粒子速度方向与x轴正方向夹角为30°.试求圆形匀强磁场区域的最小面积(不考虑粒子重力).
如图所示,一质量为m、带电荷量为+q的粒子,速度大小为v0、方向沿y轴正方向,从O点射入圆形匀强磁场区域.磁场的感应强度为B,磁场方向垂直纸面向外.粒子飞出磁场区域后,从b处穿过x轴,在b点粒子速度方向与x轴正方向夹角为30°.试求圆形匀强磁场区域的最小面积(不考虑粒子重力).