题目内容
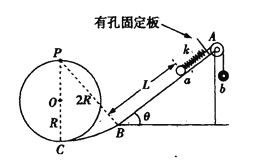
【题目】如图所示，半径为R的竖直圆轨道与半径为2R的竖直圆弧轨道BC相切于最低点C，倾角θ=37°的倾斜轨道AB与圆弧轨道BC相切于B点，将一劲度系数为k的轻质弹簧的一端固定在AB轨道上，平行于斜面的细线穿过有孔固定板和弹簧并跨过定滑轮将小球a和小球b连接，小球a与弹簧接触但不相连，小球a的质量为m，小球b的质量为
，初始时两小球静止，小球a与B点的距离为L，已知弹簧被压缩时的弹性势能表达式为
（x为弹簧压缩量），现将细线突然烧断，一切摩擦均不计，sin37°=0.6，cos37°=0.8，重力加速度为g。
（1）求细线断开的瞬间，小球a和小球b的加速度大小之比。
（2）如果小球a恰好能在圆轨道内完成竖直平面内的圆周运动，则L和R应满足什么关系？
（3）在满足第（2）问的条件下，小球a通过C点时对轨道的压力的变化量是多少？
【答案】（1）
（2）
（3）
【解析】（1）细线为断开时，由受力平衡有
解得
细线断开的瞬间，对小球a： 
，
解得： 
对小球b： 
解得
， 所以
（2）细线断开后小球a恰好能够运动到圆轨道的最高点P，由机械能守恒定律有
在最高点： 
, 
解得L=
（3）设小球a运动到C点时速度为
，
由机械能守恒定律有
解得
在C点的右侧时，圆弧轨道的半径为2R，
由牛顿第二定律： 
解得
在C点的左侧时，圆弧轨道的半径为R，
由牛顿第二定律： 
解得
故小球a通过C点时对轨道的压力的变化量为
。
练习册系列答案
相关题目
