题目内容
15.2014年5月10日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,三者几乎成一条直线.若土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆.设土星公转周期为T1,公转半径为R1;地球公转周期为T2,公转半径为R2,万有引力常量为G.忽略土星与地球之间的引力作用,从发生“土星冲日”天象开始计时,下列说法正确的是( )| A. | 土星公转速度大于地球公转速度 | |
| B. | 太阳的质量为$\frac{4{π}^{2}{{R}_{1}}^{3}}{G{{T}_{2}}^{2}}$ | |
| C. | 地球与土星相距最近经历的时间至少为$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$ | |
| D. | 土星与地球公转的向心加速度之比为$\frac{{{R}_{1}}^{2}}{{{R}_{2}}^{2}}$ |
分析 根据环绕速度公式v=$\sqrt{\frac{GM}{r}}$,列式比较线速度大小;两次发生“土星冲日”的美丽天象的时间内,地球多转动1圈;对地球,根据万有引力等于向心力列式求解太阳的质量;根据万有引力等于向心力列式求解加速度之比.
解答 解:A、地球和土星均绕太阳做匀速圆周运动,根据环绕速度公式v=$\sqrt{\frac{GM}{r}}$,轨道半径越大,线速度越小,故土星公转速度小于地球公转速度,故A错误;
B、地球做匀速圆周运动,根据牛顿第二定律,有:G$\frac{Mm}{{R}_{2}^{2}}$=m$\frac{4{π}^{2}}{{T}_{2}^{2}}{R}_{2}$,得太阳的质量M=$\frac{4{π}^{2}{R}_{2}^{3}}{G{T}_{2}^{2}}$,故B错误;
C、两次发生“土星冲日”的美丽天象的时间内,地球多转动1圈,故:
(ω1-ω2)t=2π
即:($\frac{2π}{{T}_{2}}$-$\frac{2π}{{T}_{1}}$)t=2π
解得:t=$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$.故C正确;
D、根据G$\frac{Mm}{{R}^{2}}$=ma,有:a=$\frac{GM}{{R}^{2}}$∝$\frac{1}{{R}^{2}}$,故土星与地球公转的向心加速度之比为:$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{R}_{2}^{2}}{{R}_{1}^{2}}$,故D错误;
故选:C.
点评 本题是万有引力与圆周运动知识相综合的问题,关键是明确行星的动力学原理,根据万有引力等于向心力和向心力的不同表达形式列式分析.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
10.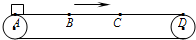 如图所示,水平传送带向右匀速转动,某时刻将小物块m轻轻放在传送带左端A点,物块在AB段做加速运动,BC段做匀速运动,到达C点时传送带开始减速,使物块在CD段做减速运动,下列情况可能出现的是( )
如图所示,水平传送带向右匀速转动,某时刻将小物块m轻轻放在传送带左端A点,物块在AB段做加速运动,BC段做匀速运动,到达C点时传送带开始减速,使物块在CD段做减速运动,下列情况可能出现的是( )
 如图所示,水平传送带向右匀速转动,某时刻将小物块m轻轻放在传送带左端A点,物块在AB段做加速运动,BC段做匀速运动,到达C点时传送带开始减速,使物块在CD段做减速运动,下列情况可能出现的是( )
如图所示,水平传送带向右匀速转动,某时刻将小物块m轻轻放在传送带左端A点,物块在AB段做加速运动,BC段做匀速运动,到达C点时传送带开始减速,使物块在CD段做减速运动,下列情况可能出现的是( )| A. | 物块在AB段受到向右的静摩擦力的作用 | |
| B. | 物块在BC段不受摩擦力的作用 | |
| C. | 物块在CD段受到向左的静摩擦力的作用 | |
| D. | 物块在CD段受到向左的滑动摩擦力的作用 |
7.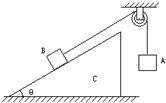 如图所示,足够长的粗糙斜面体C置于水平面上,B置于斜面上,按住B不动,B通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,放手后B沿斜面加速上滑,C一直处于静止状态.则在A落地前的过程中( )
如图所示,足够长的粗糙斜面体C置于水平面上,B置于斜面上,按住B不动,B通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,放手后B沿斜面加速上滑,C一直处于静止状态.则在A落地前的过程中( )
 如图所示,足够长的粗糙斜面体C置于水平面上,B置于斜面上,按住B不动,B通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,放手后B沿斜面加速上滑,C一直处于静止状态.则在A落地前的过程中( )
如图所示,足够长的粗糙斜面体C置于水平面上,B置于斜面上,按住B不动,B通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,放手后B沿斜面加速上滑,C一直处于静止状态.则在A落地前的过程中( )| A. | A的重力势能的减少量等于B的机械能的增加量 | |
| B. | C一定受到水平面的摩擦力 | |
| C. | 水平面对C的支持力小于B、C的总重力 | |
| D. | A物体落地前的瞬间受到绳子拉力的功率与其重力的功率相等 |
5.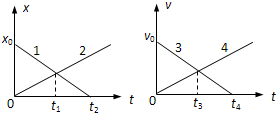 物体的运动可以用图象描述,在如图所示的x-t和v-t图象中,分别给出了a、b、c、d四个物体做直线运动所对应的图象1、2、3、4.则关于这四个运动,下列说法是正确的是( )
物体的运动可以用图象描述,在如图所示的x-t和v-t图象中,分别给出了a、b、c、d四个物体做直线运动所对应的图象1、2、3、4.则关于这四个运动,下列说法是正确的是( )
 物体的运动可以用图象描述,在如图所示的x-t和v-t图象中,分别给出了a、b、c、d四个物体做直线运动所对应的图象1、2、3、4.则关于这四个运动,下列说法是正确的是( )
物体的运动可以用图象描述,在如图所示的x-t和v-t图象中,分别给出了a、b、c、d四个物体做直线运动所对应的图象1、2、3、4.则关于这四个运动,下列说法是正确的是( )| A. | a、b一定在t1时刻相遇 | |
| B. | c、d一定在t3时刻相遇 | |
| C. | a、b运动方向相同,c、d运动方向相同 | |
| D. | a、b运动方向相反,c、d运动方向相反 |
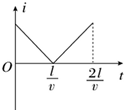
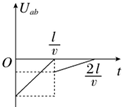
 如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧,的I、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a方向的感应电流为正,则在线圈穿过磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )
如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧,的I、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a方向的感应电流为正,则在线圈穿过磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )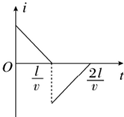

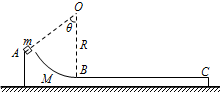 如图所示,静止在水平面上的弧形木板质量为2m,AB部分是半径为R、圆心角θ=53°的圆弧轨道,BC部分是长为L的水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.已知物块与弧形木板间的动摩擦因数为μ,sin53°=0.8,cos53°=0.6,重力加速度为g.求:
如图所示,静止在水平面上的弧形木板质量为2m,AB部分是半径为R、圆心角θ=53°的圆弧轨道,BC部分是长为L的水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.已知物块与弧形木板间的动摩擦因数为μ,sin53°=0.8,cos53°=0.6,重力加速度为g.求: