题目内容
8.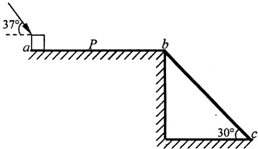 如图所示,水平平台ab长为20m,平台b端与长度未知的特殊材料制成的斜面bc连接,斜面倾角为30°.在平台b端放上质量为5kg的物块,并给物块施加与水平方向成37°角的50N推力后,物块由静止开始运动.己知物块与平台间的动摩擦因数为0.4,重力加速度g=10m/s2,sin37°=0.6,求:(第(2)、(3)两问结果保留三位有效数字)
如图所示,水平平台ab长为20m,平台b端与长度未知的特殊材料制成的斜面bc连接,斜面倾角为30°.在平台b端放上质量为5kg的物块,并给物块施加与水平方向成37°角的50N推力后,物块由静止开始运动.己知物块与平台间的动摩擦因数为0.4,重力加速度g=10m/s2,sin37°=0.6,求:(第(2)、(3)两问结果保留三位有效数字) (1)物块由a运动到b所用的时间;
(2)若物块从a端运动到P点时撤掉推力,则物块刚好能从斜面b端开始下滑,则间aP的距离为多少?(物块在b端无能量损失)
(3)若物块与斜面间的动摩擦因数μbc=0.277+0.03Lb,式中Lb为物块在斜面上所处的位置离b端的距离,在(2)中的情况下,物块沿斜面滑到什么位置时速度最大?
分析 (1)根据牛顿运动定律求解加速度,根据位移时间关系知时间;
(2)根据位移速度关系列方程求解;
(3)物体沿斜面下滑的速度最大时,须加速度为0,根据受力分析列方程,结合物块与斜面间的动摩擦因数μbc=0.277+0.03Lb知斜面长度的临界值,从而讨论最大速度.
解答 解:(1)受力分析知物体的加速度为
a1=$\frac{Fcos37°-μ(Fsin37°+mg)}{m}$=$\frac{50×0.8-0.4(50×0.6+50)}{{5}^{2}}$=1.6m/s2
x=$\frac{1}{2}$a1t2
解得a到b的时间为t=$\sqrt{\frac{2×20}{1.6}}$=5s
(2)物体从a到p:${v}_{p}^{2}$=2a1x1
物块由P到b:${v}_{p}^{2}$=2a2x2
a2=μg
x=x1+x2
解得ap距离为x1=14.3m
(3)物体沿斜面下滑的速度最大时,须加速度为0,
即a=$\frac{mgsinθ-μmgcosθ}{m}$=0
μbc=0.277+0.03Lb,
联立解得Lb=10m
因此如斜面长度L>10m,则Lb=10m时速度最大;
若斜面长度L≤10m,则斜面最低点速度最大.
答:(1)物块由a运动到b所用的时间为5s;
(2)若物块从a端运动到P点时撤掉推力,则物块刚好能从斜面b端开始下滑,则间aP的距离为14.3m;
(3)斜面长度L>10m,则Lb=10m时速度最大;若斜面长度L≤10m,则斜面最低点速度最大.
点评 本题考查的是牛顿第二定律及共点力平衡,但是由于涉及到动摩擦因数变化,增加了难度;故在分析时要注意物体沿斜面下滑的速度最大时,须加速度为0这个条件.

练习册系列答案
相关题目
18.下列射线中,来自于原子核内部,且穿透能力最强的射线是( )
| A. | γ射线 | B. | α射线 | C. | 阴极射线 | D. | X射线 |
13.在进行飞镖训练时,打飞镖的靶上共标有10环,且第10环的半径最小,为1cm,第9环的半径为2 cm,…,以此类推,若靶的半径为10cm,当人离靶的距离为5m,将飞镖对准10环中心以水平速度v投出,g=10m/s2.则下列说法中,不正确的是( )
| A. | 当v≥50 m/s时,飞镖将射中第8环线以内 | |
| B. | 当v≥50 m/s时,飞镖将射中第6环线内 | |
| C. | 若要击中第10环的圆内,飞镖的速度v至少应为50$\sqrt{5}$ m/s | |
| D. | 若要击中靶子,飞镖的速度v至少应为25$\sqrt{2}$ m/s |
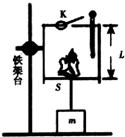 为研究我国传统的治病工具--拔火罐的工作原理,某同学设计了如图实验.圆柱状气缸被固定在铁架台上,气缸横截面积S=30cm2,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,测出此时缸内温度为127℃.活塞通过不可伸长的细线与重物m相连,此时活塞下的细线刚好拉直且拉力为零.而这时活塞距缸底为L.由于气缸导热良好,重物被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,大气压强为1.0×105Pa,g取10m/s2,气缸内的气体可看做理想气体,活塞与细线的质量不计.求:
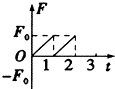
为研究我国传统的治病工具--拔火罐的工作原理,某同学设计了如图实验.圆柱状气缸被固定在铁架台上,气缸横截面积S=30cm2,将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内,酒精棉球熄灭时密闭开关K,测出此时缸内温度为127℃.活塞通过不可伸长的细线与重物m相连,此时活塞下的细线刚好拉直且拉力为零.而这时活塞距缸底为L.由于气缸导热良好,重物被吸起,最后重物稳定在距地面$\frac{L}{10}$处.已知环境温度为27℃不变,大气压强为1.0×105Pa,g取10m/s2,气缸内的气体可看做理想气体,活塞与细线的质量不计.求: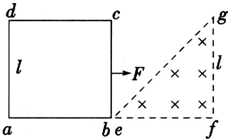 在光滑水平桌面上有一边长为l的正方形线框abcd,bc边右侧有一等腰直角三角形匀强磁场区域efg,三角形腰长为l,磁感应强度竖直向下,a、b、e、f在同一直线上,其俯视图如图所示,线框从图示位置在水平拉力F作用下以速度v向右匀速穿过磁场区,线框中感应电流i-t和F-t图象正确的是(以逆时针方向为电流的正方向,以水平向右的拉力为正,时间单位为$\frac{l}{t}$)( )
在光滑水平桌面上有一边长为l的正方形线框abcd,bc边右侧有一等腰直角三角形匀强磁场区域efg,三角形腰长为l,磁感应强度竖直向下,a、b、e、f在同一直线上,其俯视图如图所示,线框从图示位置在水平拉力F作用下以速度v向右匀速穿过磁场区,线框中感应电流i-t和F-t图象正确的是(以逆时针方向为电流的正方向,以水平向右的拉力为正,时间单位为$\frac{l}{t}$)( )
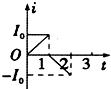

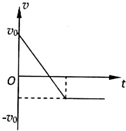
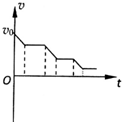
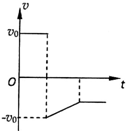
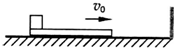 如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )
如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )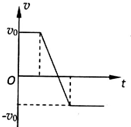

 某同学只记录了A、B、C三点,各点的坐标如图所示,则物体运动的初速度为1m/s,开始平抛的初始位置的坐标为(-10cm,-5cm).
某同学只记录了A、B、C三点,各点的坐标如图所示,则物体运动的初速度为1m/s,开始平抛的初始位置的坐标为(-10cm,-5cm).