题目内容
【题目】如图所示为用绞车拖物块的示意图。拴接物块的细线被缠绕在轮轴上,轮轴逆时针转动从而拖动物块。已知轮轴的半径R=0.5m,细线始终保持水平;被拖动的物块初速度为零质量m=1kg,与地面间的动摩擦因数μ=0.5;轮轴的角速度随时间t变化的关系是ω=kt,k=2rad/s2,g取10m/s2,以下判断正确的是( )
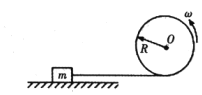
A.物块的加速度逐渐增大
B.细线对物块的拉力恒为5N
C.![]() 时,细线对物块的拉力的瞬时功率为12W
时,细线对物块的拉力的瞬时功率为12W
D.前2秒内,细线对物块拉力做的功为6J
【答案】C
【解析】
A、轮轴边缘的线速度大小等于物体的速度大小,根据线速度好角速度的关系,有v=Rω=Rkt,可见物体做匀加速直线运动,加速度a=Rk=0.5×2m/s2=1m/s2;故A错误.
B、对物体,根据牛顿第二定律:F-μmg=ma,代入数据解得F=6N;故B错误.
C、t=2s时,物体的速度为v=at=1×2m/s=2m/s,细线对物块的拉力的瞬时功率为P=Fv=2×6W=12W;故C正确.
D、前2秒内,物体的位移![]() ,细线对物块拉力做的功为W=Fs=6×2J=12J;故D错误.
,细线对物块拉力做的功为W=Fs=6×2J=12J;故D错误.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目