题目内容
18. 如图所示,有一竖直放置的“T”形架,表面光滑,滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻绳相连,A、B质量相等,且可看做质点.开始时细绳水平伸直,A、B静止.由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v时,则A的速度为( )
如图所示,有一竖直放置的“T”形架,表面光滑,滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻绳相连,A、B质量相等,且可看做质点.开始时细绳水平伸直,A、B静止.由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v时,则A的速度为( )| A. | v | B. | $\frac{1}{2}$v | C. | $\frac{\sqrt{3}}{2}$v | D. | $\frac{\sqrt{3}}{3}$v |
分析 将A、B的速度分解为沿绳子方向和垂直于绳子方向,抓住沿绳子方向的速度相等,结合平行四边形定则求出A的速度,继而可知各选项的正误.
解答  解:A、B的速度分解如图所示,滑块B沿绳子方向上的分速度为:v1=vcos60°
解:A、B的速度分解如图所示,滑块B沿绳子方向上的分速度为:v1=vcos60°
滑块A沿绳子方向上的速度为:vA1=vAsin60°
因为v1=vA1
则有:vA=vcot60°=$\frac{\sqrt{3}}{3}$v.故D正确,A、B、C错误.
故选:D.
点评 该题是考察了关于连接体的问题,对于此类问题,找出相联系的两个物体的共同的物理量是解题的关键,解决本题的关键就是抓住沿绳子方向的分速度相等,然后再结合平行四边形定则即可求解.该题还要会熟练的应用三角函数解答相关的物理问题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.影响物质材料电阻率的因素很多,一般金属材料的电阻率随温度的升高而增大,而半导体材料的电阻率则与之相反,随温度的升高而减小.某课题研究组需要研究某种导电材料的导电规律,他们用该种导电材料制作成电阻较小的线状元件Z做实验,测量元件Z中的电流随两端电压从零逐渐增大过程中的变化规律.
(1)他们应选用图1所示的哪个电路进行实验?答:A
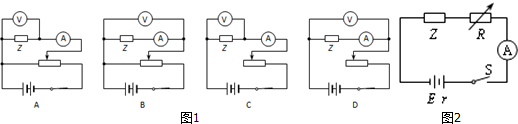
(2)实验测得元件Z的电压与电流的关系如表所示.根据表中数据,判断元件Z是金属材料还是半导体材料?答:半导体.
(3)把元件Z接入如图2所示的电路中,当电阻R的阻值为R1=2Ω时,电流表的读数为1.25A;当电阻R的阻值为R2=3.6Ω时,电流表的读数为0.80A.结合上表数据,求出电池的电动势为4.0V,内阻为0.40Ω.(不计电流表的内阻,结果保留两位有效数字)
(1)他们应选用图1所示的哪个电路进行实验?答:A

(2)实验测得元件Z的电压与电流的关系如表所示.根据表中数据,判断元件Z是金属材料还是半导体材料?答:半导体.
| U(V) | 0 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.50 | 1.60 |
| I(A) | 0 | 0.20 | 0.45 | 0.80 | 1.25 | 1.80 | 2.81 | 3.20 |
13.随着MP4播放器的出现,人们可以在旅途中观看电影,让原本枯燥的旅途变得充满乐趣.MP4的充电电流多为锂电池,假设锂电池的充电电流为300mA,则以下说法正确的是( )
| A. | 1s通过电池某一横截面的电量为300C | |
| B. | 1s通过电池某一横截面的电量为0.3C | |
| C. | 充电过程把其他形式的能转化为电能 | |
| D. | 充电过程把电能转化为其他形式的能 |
3.如图所示,在人的牵引下使船靠岸,为使船能匀速靠岸,则此人牵引绳的速度应( )


| A. | 大小不变 | B. | 逐渐减小 | C. | 逐渐增大 | D. | 先减小后增大 |
10.两颗人造卫星绕地球做匀速圆周运动,它们的质量之比为mA:mB=1:2,轨道半径之比为rA:rB=3:1,则下列说法中不正确的是( )
| A. | 它们的线速度之比为vA:vB=1:$\sqrt{3}$ | |
| B. | 它们的向心加速度之比为aA:aB=1:9 | |
| C. | 它们的向心力之比为FA:FB=1:18 | |
| D. | 它们的周期之比为TA:TB=3:1 |
8.一个物体静止在水平桌面上,下列说法正确的是( )
| A. | 物体对桌面的压力就是物体的重力 | |
| B. | 桌面对物体的支持力和物体对桌面的压力是一对作用力与反作用力 | |
| C. | 桌面对物体的支持力和物体对桌面的压力是一对平衡力 | |
| D. | 桌面对物体的支持力和物体对桌面的压力,它们产生作用效果可以抵消 |
 如图所示,质量为m=0.2kg的小球固定在长为L=0.5m的轻杆的一端,杆可绕O点的水平转轴在竖直平面内转动.小球过最高点时的速度为V=4m/s,不计阻力(g=10m/s2).求:
如图所示,质量为m=0.2kg的小球固定在长为L=0.5m的轻杆的一端,杆可绕O点的水平转轴在竖直平面内转动.小球过最高点时的速度为V=4m/s,不计阻力(g=10m/s2).求: