题目内容
【题目】如图所示为某自动控制系统的装置示意图,装置中间有一个以v0=3m/s的速度逆时针匀速转动的水平传送带,传送带左端点M与光滑水平面相切,水平面左侧与一倾角α=37°的光滑斜面平滑连接。靠近斜面底端的P点处安装有自动控制系统,当小物块b每次向右经过P点时都会被系统瞬时锁定从而保持静止。传送带N端与半径r=0.2m的光滑四分之一圆弧相切,小物块α从圆弧最高点由静止下滑后滑过传送带,经过M点后控制系统会使静止在P点的小物块b自动解锁,之后两物块发生第一次弹性碰撞。已知两物块的质量mb=2ma=2kg,两物块均可视为质点,物块与传送带间的动摩擦因数μ=0.25,MN间的距离L=1.2m, g=10m/s2,sin37°=0.6,cos37°=0.8,求:
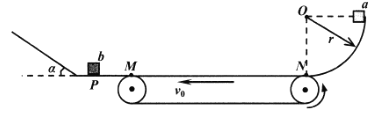
(1)物块a运动到N点时受到的支持力;
(2)物块b第一次沿斜面上滑的时间;
(3)两物块在第n次碰撞后到第n+1次碰撞前,物块a在传送带上运动产生的摩擦热。
【答案】(1)30N (2)![]() (3)
(3)![]()
【解析】本题考查传送带与弹性碰撞相结合问题,涉及功能关系与动量定理的应用。
(1)对物块a沿圆弧从最高点由静止下滑到N点,运用动能定理可得:![]() ,解得
,解得![]()
对物块a运动到N点时,受力分析由牛顿第二定律可得![]() ,解得
,解得![]()
(2)小球a在传送带上运动的加速度![]()
设小球a加速到3m/s前进的距离为x,则![]()
故小球a到达M点的速度为v2=3m/s
设两球第一次碰撞后获得的速度为val、vbl,因碰撞是弹性碰撞,则
![]() 、
、![]()
解得:![]()
![]()
对物块b第一次沿斜面上滑,应用动量定理可得![]()
解得:![]()
(3)小球a第一次向右在传送带上通过的位移:![]()
小球a第一次向右在传送带上向右运动的时间:![]()
因此小球a从传送带上返回再次与静止的b球发生碰撞。经过n次碰撞后小球a获得的速度:![]()
小球a与传送带间的相对位移:![]()
故生成的热量![]()