题目内容
19.在做“研究平抛物体的运动”的实验时,利用如图所示的装置,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹并计算平抛运动的初速度: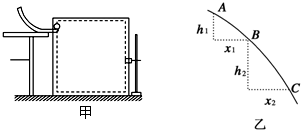
(1)安装实验装置的过程中,斜槽末端的切线必须是水平的,这样做的目的是B
A.保证小球飞出时,速度既不太大,也不太小
B.保证小球飞出时,初速度水平
C.保证小球在空中运动的时间每次都相等
D.保证小球运动的轨迹是一条抛物线
(2)为了能准确地描绘小球的运动轨迹,下面列出了一些操作要求,将你认为正确的选项填在横线上BDE
A.每次释放小球的位置必须不同
B.每次必须由静止释放小球
C.斜槽轨道的末端点是平抛运动的初位置
D.木板要用眼睛目测调整为竖直
E.将球的位置记录在纸上后,取下纸,用平滑的曲线连接各点
(3)某同学在描绘平抛运动轨迹时,得到的部分轨迹曲线如图乙所示.在 曲线上取A、B、C三个点,测量得到A、B、C三点间竖直距离h1=9.20cm,h2=49.20cm,A、B、C三点间水平距离x1=x2=20.40cm,g=10m/s2,则:小球从A点运动到B点的时间为0.2s,及小球做平抛运动的初速度大小为1.02m/s.(结果保留小数点后两位)
分析 (1、2)保证小球做平抛运动必须通过调节使斜槽的末端保持水平,因为要画同一运动的轨迹,必须每次释放小球的位置相同,且由静止释放,以保证获得相同的初速度,实验要求小球滚下时不能碰到木板平面,避免因摩擦而使运动轨迹改变,最后轨迹应连成平滑的曲线;
(3)平抛运动可以分解为水平方向的运算直线运动与竖直方向的自由落体运动,在竖直方向上应用匀变速运动的推论求出小球的运动时间,然后由运算运动规律求出小球的初速度.
解答 解:(1)研究平抛运动的实验很关键的地方是要保证小球能够水平飞出,只有水平飞出时小球才做平抛运动,故ACD错误,B正确.
故选:B.
(2)A、因为要画同一运动的轨迹,必须每次释放小球的位置相同,且由静止释放,以保证获得相同的初速度.故A错误,B正确;
C、小球放在轨道末端时球心的位置才是平抛运动的初位置,故C错误;
D、固定白纸的木板必须调节成竖直.故D正确.
E、实验要求小球滚下时不能碰到木板平面,避免因摩擦而使运动轨迹改变,最后轨迹应连成平滑的曲线.故E正确.
故选:BDE
(3)小球的水平距离x1=x2=20.40cm,则小球从A到B的运动时间与从B到C的运动时间相等,
在竖直方向上,小球做自由落体运动,△h=gt2,则t=$\sqrt{\frac{△h}{g}}=\sqrt{\frac{0.492-0.0920}{10}}=0.2s$,
小球的初速度v0=$\frac{{x}_{1}}{t}=\frac{0.2040}{0.2}=1.02$m/s;
故答案为:(1)B;(2)BDE;(3)0.2;1.02
点评 在实验中如何实现让小球做平抛运动是关键,因此实验中关键是斜槽末端槽口的切线保持水平及固定后的斜槽要竖直.对于平抛运动问题,一定明确其水平和竖直方向运动特点,尤其是在竖直方向熟练应用匀变速直线运动的规律和推论解题.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案 如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )
如图一木块放在水平桌面上,在水平外力F2=3N,F1=8N和作用下处于静止状态,若撤去力F1,则木块在水平方向受到的摩擦力为( )| A. | 8N、向左 | B. | 8N、向左 | C. | 3N、向右 | D. | 3N、向左 |
| A. | 合运动的轨迹一定是抛物线 | |
| B. | 合运动的性质一定是匀变速运动 | |
| C. | 合运动一定是匀变速直线运动 | |
| D. | 任意相等时间间隔△t内合速度的增量一定相等 |
| A. | 缓慢抽出纸条,笔帽受到的摩擦力大 | |
| B. | 快速抽出纸条,笔帽受到的摩擦力大 | |
| C. | 缓慢抽出纸条,笔帽受到的冲量大 | |
| D. | 快速抽出纸条,笔帽受到的冲量大 |
| A. | 9 N | B. | 12 N | C. | 3 N | D. | 10 N |
| A. | 只有重力 | B. | 重力和下滑力 | ||
| C. | 重力和斜面对它的弹力 | D. | 重力,斜面对它的弹力及下滑力 |
| A. | 物体的加速度大,则速度变化一定快 | |
| B. | 物体的加速度为零,则速度也为零 | |
| C. | 物体的加速度大,则速度也大 | |
| D. | 物体的加速度的方向就是速度的方向 |
 如图所示,一物体以一初速度滑上斜面,已知物体重20N,斜面倾角θ为30°,物体与斜面的动摩擦因数μ为0.5,则物体上滑过程中,
如图所示,一物体以一初速度滑上斜面,已知物体重20N,斜面倾角θ为30°,物体与斜面的动摩擦因数μ为0.5,则物体上滑过程中,