Question

【题目】水平粗糙直轨道ab与半径为R的竖直半圆形光滑轨道bc平滑相接于b点，一质量为m的小滑块以初速度v0从a点开始，沿轨道ab向右运动，如图所示，小滑块进入半圆形轨道后刚好能通过最高点c，并落到水平地面上d点（不计空气阻力，重力加速度为g）

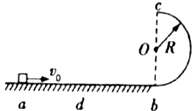
（1）求bd两点之间的距离x；

（2）求小滑块经过半圆形轨道b点处时对轨道的压力F的大小．

（3）若小滑块质量变为2m，依然从a点出发，刚好能通过最高点c，则初速度v为多少？

Answer 1

【答案】（1）2R（2）6mg （3）v0

【解析】

试题分析：（1）由小滑块开始时能够经过最高点可得：

x=vct 2R=gt2

解得x=2R

（2）小滑块从b点到c点由动能定理：

小滑块在b点处时，由牛顿第二定律可得：，

解得F/=6mg

由牛顿第三定律可知，小滑块对轨道的压力为F=6mg

（3）设ab段长度为L，小滑块与轨道间的动摩擦因数为μ，则当质量为m时

在L和μ确定的前提下，该方程的成立与小滑块的质量无关，当质量变为2m时，初速度依然为v0，即v=v0．