题目内容
 如图所示,光滑小球从a处无初速度释放,它可以直接下落,也可以沿光滑斜面ac、ad、ae滑到传送带上,已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°,传送带与水平方向的夹角θ=30°,则小球以最短的时间到达传送带的路径是
如图所示,光滑小球从a处无初速度释放,它可以直接下落,也可以沿光滑斜面ac、ad、ae滑到传送带上,已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°,传送带与水平方向的夹角θ=30°,则小球以最短的时间到达传送带的路径是
- A.ab
- B.ac
- C.ad
- D.ae
B
分析:根据牛顿第二定律求出在斜面上运动的加速度大小,根据几何关系求出斜面的长度,再根据x= 判断运动时间的长短.
判断运动时间的长短.
解答:设ac的长度为x,知ab、ad的长度相同,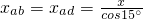 ,
,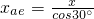 .根据牛顿第二定律得,ab=g,ac=gsin75°,ad=gsin60°,ae=gsin45°.
.根据牛顿第二定律得,ab=g,ac=gsin75°,ad=gsin60°,ae=gsin45°.
根据x= 得,
得, ,
,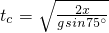 ,
,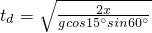 ,
,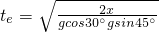 ,比较知tc最小.故B正确,A、C、D错误.
,比较知tc最小.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键正确地受力分析,运用牛顿第二定律和运动学公式进行求解.
分析:根据牛顿第二定律求出在斜面上运动的加速度大小,根据几何关系求出斜面的长度,再根据x=
 判断运动时间的长短.
判断运动时间的长短.解答:设ac的长度为x,知ab、ad的长度相同,
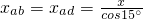 ,
,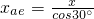 .根据牛顿第二定律得,ab=g,ac=gsin75°,ad=gsin60°,ae=gsin45°.
.根据牛顿第二定律得,ab=g,ac=gsin75°,ad=gsin60°,ae=gsin45°.根据x=
 得,
得, ,
,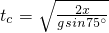 ,
,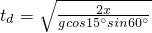 ,
,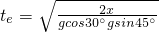 ,比较知tc最小.故B正确,A、C、D错误.
,比较知tc最小.故B正确,A、C、D错误.故选B.
点评:解决本题的关键正确地受力分析,运用牛顿第二定律和运动学公式进行求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
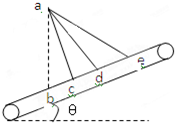 如图所示,光滑小球从a处无初速度释放,它可以直接下落,也可以沿光滑斜面ac、ad、ae滑到传送带上,已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°,传送带与水平方向的夹角θ=30°,则小球以最短的时间到达传送带的路径是( )
如图所示,光滑小球从a处无初速度释放,它可以直接下落,也可以沿光滑斜面ac、ad、ae滑到传送带上,已知ac、ad、ae与竖直方向的夹角分别是15°、30°、45°,传送带与水平方向的夹角θ=30°,则小球以最短的时间到达传送带的路径是( )


