题目内容
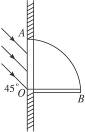
 如图所示,AOB是1/4圆柱玻璃砖的截面,一束平行光以45°入射角射入玻璃砖的OA面,OA面以外的光线均被挡光板吸收.假设玻璃砖对此光线的折射率n=
如图所示,AOB是1/4圆柱玻璃砖的截面,一束平行光以45°入射角射入玻璃砖的OA面,OA面以外的光线均被挡光板吸收.假设玻璃砖对此光线的折射率n=| 2 |
分析:画出光路图,当光线在AB弧面上发生全反射时,就没有光线从AB弧面射出,根据临界角确定出光线在AB弧面上恰好发生全反射时的入射点,由几何知识求解圆柱AB面上能射出光线的面积占AB表面积的几分之几.
解答:解:由 sinC=
得临界角为:C=45°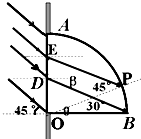
如图,设射到D点的光线刚好折射到B点
由折射定律有:
=n
解得:β=30°
D点以下的光线射到OB面上被吸收.
设射到E点的光线折射到P点刚好全反射
E点以上的光线射到圆弧面被全反射
由几何关系不难求出:θ=15°
弧长lPB=
lAB,
答:AB面上能射出光线部分占AB表面的
.
| 1 |
| n |

如图,设射到D点的光线刚好折射到B点
由折射定律有:
| sin45° |
| sinβ |
解得:β=30°
D点以下的光线射到OB面上被吸收.
设射到E点的光线折射到P点刚好全反射
E点以上的光线射到圆弧面被全反射
由几何关系不难求出:θ=15°
弧长lPB=
| 1 |
| 6 |
答:AB面上能射出光线部分占AB表面的
| 1 |
| 6 |
点评:正确地画出光路图是解决本题问题的关键,是折射定律和几何知识的结合应用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
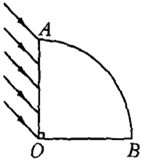 如图所示,AOB是1/4圆柱玻璃砖的截面图,玻璃的折射率为
如图所示,AOB是1/4圆柱玻璃砖的截面图,玻璃的折射率为 如图所示,AOB是1/4圆柱玻璃砖的截面图,玻璃的折射率为
如图所示,AOB是1/4圆柱玻璃砖的截面图,玻璃的折射率为