题目内容
(2008?潍坊模拟)“嫦娥奔月”的过程可以简化为:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,在远地点时的速度为v,然后经过变轨被月球捕获,再经多次变轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动.
(1)已知地球半径为R1、表面的重力加速度为g0,求“嫦娥一号”在远地点A处的万有引力产生的加速度a的大小;
(2)已知月球的质量为M、半径为R2,引力常量为G,求“嫦娥一号”绕月球运动的周期T.
(1)已知地球半径为R1、表面的重力加速度为g0,求“嫦娥一号”在远地点A处的万有引力产生的加速度a的大小;
(2)已知月球的质量为M、半径为R2,引力常量为G,求“嫦娥一号”绕月球运动的周期T.
分析:(1)嫦娥一号受到合力为地球的万有引力,由牛顿第二定律可以求出A点处的加速度.
(2)月球对嫦娥一号的万有引力提供向心力,由牛顿第二定律可以求出其绕月运动的周期.
(2)月球对嫦娥一号的万有引力提供向心力,由牛顿第二定律可以求出其绕月运动的周期.
解答:解:(1)由牛顿第二定律得:
对嫦娥一号卫星:ma=G
=G
,
在地球表面的物体mg0=G
,
解得:a=
;
(2)月球的万有引力提供向心力,
由牛顿第二定律得:G
=m(
)2(R2+h2),
解得,嫦娥一号绕月运动的周期T=2π
;
答:(1)“嫦娥一号”在远地点A处的万有引力产生的加速度为
;
(2)“嫦娥一号”绕月球运动的周期2π
.
对嫦娥一号卫星:ma=G
| Mm |
| r2 |
| Mm |
| (R1+h1)2 |
在地球表面的物体mg0=G
| Mm |
| R12 |
解得:a=
| ||
| (R1+h1)2 |
(2)月球的万有引力提供向心力,
由牛顿第二定律得:G
| Mm |
| (R2+h2)2 |
| 2π |
| T |
解得,嫦娥一号绕月运动的周期T=2π
|
答:(1)“嫦娥一号”在远地点A处的万有引力产生的加速度为
| ||
| (R1+h1)2 |
(2)“嫦娥一号”绕月球运动的周期2π
|
点评:万有引力等于重力,万有引力提供向心力,由万有引力定律及牛顿第二定律可以正确解题.

练习册系列答案
相关题目
 (2008?潍坊模拟)半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止.则在此过程中,下列说法中正确的是( )
(2008?潍坊模拟)半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止.则在此过程中,下列说法中正确的是( )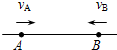 (2008?潍坊模拟)如图所示的直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一带正电粒子以速度vA经过A点向B点运动,经过一段时间后,粒子以速度vB经过B点,且vB与vA方向相反,不计粒子重力,下面说法正确的是( )
(2008?潍坊模拟)如图所示的直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一带正电粒子以速度vA经过A点向B点运动,经过一段时间后,粒子以速度vB经过B点,且vB与vA方向相反,不计粒子重力,下面说法正确的是( )