题目内容
3.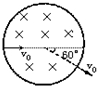 如图所示,带负电的粒子垂直磁场方向进入圆形匀强磁场区域,出磁场时速度偏离原方向60°角,已知带电粒子质量m,电量q,速度v0,磁场区域的半径R,不计重力,求:
如图所示,带负电的粒子垂直磁场方向进入圆形匀强磁场区域,出磁场时速度偏离原方向60°角,已知带电粒子质量m,电量q,速度v0,磁场区域的半径R,不计重力,求:(1)磁场的磁感应强度B;
(2)粒子在磁场中的运动时间t.
分析 (1)带负电的粒子垂直磁场方向进入圆形匀强磁场区域,由洛伦兹力提供向心力,由几何知识求出轨迹半径r,根据牛顿第二定律求出磁场的磁感应强度.
(2)根据粒子转过的圆心角与粒子做圆周运动的周期求出粒子在磁场中的运动时间.
解答  解:(1)粒子运动轨迹如图所示:
解:(1)粒子运动轨迹如图所示:
由几何知识得知,粒子转过的圆心角:θ=60°,
粒子做圆周运动的轨道半径:r=Rcot30°=$\sqrt{3}$R,
粒子做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:B=$\frac{\sqrt{3}m{v}_{0}}{3qR}$
(2)粒子做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中的运动时间:t=$\frac{θ}{360°}$T=$\frac{1}{6}$T,
解得:t=$\frac{\sqrt{3}πR}{6{v}_{0}}$
答:(1)磁场的磁感应强度为$\frac{\sqrt{3}m{v}_{0}}{3qR}$;
(2)带电粒子在磁场中运动的时间为$\frac{\sqrt{3}πR}{6{v}_{0}}$.
点评 本题是带电粒子在匀强磁场中运动的问题,画轨迹是关键,是几何知识和动力学知识的综合应用,常规问题.

练习册系列答案
相关题目
13.如图所示,是一质点作直线运动的v-t图象,下列说法中不正确的是( )


| A. | 整个过程中,18-20秒段和20-22秒段的加速度数值最大 | |
| B. | 整个过程中,D点所表示的状态离出发点最远 | |
| C. | 整个过程中,14-18秒段的加速度数值最大 | |
| D. | 14-18秒段所表示的运动通过的路程是34m |
11.关于点电荷,以下说法正确的是( )
| A. | 足够小的电荷,就是点电荷 | |
| B. | 一个电子,不论在何种情况下均可视为点电荷 | |
| C. | 只有正电荷才能看成点电荷 | |
| D. | 一个带电体能否看成点电荷,不是看它尺寸的绝对值,而是看它的形状和尺寸对相互作用力的影响能否忽略不计 |
18. 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )| t/s | 0 | 2 | 4 | 6 |
| v/m•s-1 | 0 | 6 | 10 | 6 |
| A. | 物体运动过程中的最大速度为10 m/s | |
| B. | t=5 s的时刻物体恰好经过B点 | |
| C. | t=9 s的时刻物体恰好停在C点 | |
| D. | A、B间的距离大于B、C间的距离 |
8.下列关于质点的说法正确的是( )
| A. | 研究日食时,可以把太阳看成质点 | |
| B. | 研究地球的公转时,可以把地球看成质点 | |
| C. | 研究地球的自转时,可以把地球看成质点 | |
| D. | 原子核很小,必须把它看成质点 |
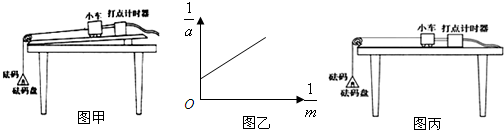
15.在“探究小车速度随时间变化的规律”的实验中,下列说法正确的是( )
| A. | 钩码的质量越大越好 | |
| B. | 在释放小车前,小车应靠近有定滑轮的一端 | |
| C. | 开始前要先开电源后放纸带,打完点要先断开电源后取纸带 | |
| D. | 坐标轴单位长度越小越好 |
12.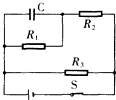 如图所示,闭合开关S,电路处于稳定状态.若突然断开开关S,则在开关S断开瞬间( )
如图所示,闭合开关S,电路处于稳定状态.若突然断开开关S,则在开关S断开瞬间( )
 如图所示,闭合开关S,电路处于稳定状态.若突然断开开关S,则在开关S断开瞬间( )
如图所示,闭合开关S,电路处于稳定状态.若突然断开开关S,则在开关S断开瞬间( )| A. | 流过电阻R1的电流可能比原来大 | B. | 流过电阻R3的电流肯定比原来小 | ||
| C. | 流过电阻R2的电流可能比原来大 | D. | 流过电阻R3的电流可能比原来大 |