题目内容
1. 如图所示,水平放置的长L=0.2m的两平行金属板相距d=0.1m,距离金属板右端水平距离也为d的位置有一足够长的屏PQ.在两板左端一粒子源能源源不断地沿两板中线发射比荷$\frac{q}{m}$=100C/kg的带电粒子,所有粒子速度大小均为v0=100m/s.当两板无电压时,粒子打在屏上O点处.若两板可以加上的电压分别为U1=10V,U2=25V,U3=100V.不计粒子间的相互作用力和粒子的重力.求:
如图所示,水平放置的长L=0.2m的两平行金属板相距d=0.1m,距离金属板右端水平距离也为d的位置有一足够长的屏PQ.在两板左端一粒子源能源源不断地沿两板中线发射比荷$\frac{q}{m}$=100C/kg的带电粒子,所有粒子速度大小均为v0=100m/s.当两板无电压时,粒子打在屏上O点处.若两板可以加上的电压分别为U1=10V,U2=25V,U3=100V.不计粒子间的相互作用力和粒子的重力.求:(1)三种电压条件下,粒子在电场中运动的最短时间tm;
(2)三种电压条件下,粒子打在PQ上的点离O点最远的距离Lm.
分析 (1)粒子在电场中作类平抛运动,水平方向匀速,竖直方向匀加速,分离开极板和打到极板分别计算出时间即可求得
(2)由粒子作类平抛运动的结论及几何关系求的
解答 解:(1)粒子在电场中作类平抛运动,有:
水平方向上位移:x=v0t①
竖直方向上位移:$y=\frac{1}{2}a{t}^{2}$②
粒子在电场中的加速度$a=\frac{qE}{m}$③
$E=\frac{U}{d}$④
当粒子恰好从两板右边缘飞出电场时有:x=L,$y=\frac{d}{2}$,
设此时两板电压U=U0,解得:U0=25V
当两板电压为U=U3=100V时,粒子将打在上极板上,此时$y=\frac{d}{2}$,粒子运动时间最短
由②③④式及$y=\frac{d}{2}$可得tn=1×10-3s
(2)当两板电压为U=U0=U2时,粒子打在PQ上的点离O点最远,
由粒子作类平抛运动的结论及几何关系有:$\frac{\frac{L}{2}}{\frac{L}{2}+d}=\frac{\frac{d}{2}}{{L}_{m}}$
解得Lm=0.1m
答:(1)三种电压条件下,粒子在电场中运动的最短时间tm为1×10-3s
(2)三种电压条件下,粒子打在PQ上的点离O点最远的距离Lm为0.1m
点评 本题主要考查了粒子在偏转电场中做类平抛运动的计算,关键是抓住水平方向匀速,竖直方向匀加速运动即可

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.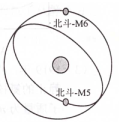 2012年12月27日,我国自行研制的“北斗导航卫星系统”(BDS)正式组网投入商用.2012年9月采用一箭双星的方式发射了该系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示.关于这两颗卫星,下列说法正确的是( )
2012年12月27日,我国自行研制的“北斗导航卫星系统”(BDS)正式组网投入商用.2012年9月采用一箭双星的方式发射了该系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示.关于这两颗卫星,下列说法正确的是( )
 2012年12月27日,我国自行研制的“北斗导航卫星系统”(BDS)正式组网投入商用.2012年9月采用一箭双星的方式发射了该系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示.关于这两颗卫星,下列说法正确的是( )
2012年12月27日,我国自行研制的“北斗导航卫星系统”(BDS)正式组网投入商用.2012年9月采用一箭双星的方式发射了该系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示.关于这两颗卫星,下列说法正确的是( )| A. | 两颗卫星的向心加速度相同 | |
| B. | 两颗卫星的速率均小于7.9m/s | |
| C. | 北斗-M6的速率小于同步卫星的速率 | |
| D. | 北斗-M5的运行周期大于地球自转周期 |
16.宇航员在探测某星球时,发现该星球带有电荷,为进一步探测,宇航员做了如下实验:将一带电量远小于星球电荷量的小球在离星球表面h高度处由静止释放,发现带电小球恰好处于悬浮状态.现在若按下列选项描述的情形改变实验条件,测小球仍处于悬浮状态的是( )
| A. | 仅改变小球的电性 | B. | 仅改变小球离星球表面的高度 | ||
| C. | 仅改变小球的电荷量 | D. | 仅改变小球的质量 |
10. 如图,球形连通容器A置于水平面上,水平部分的水银将球内气体隔开,且V1>V2.开始时两边气体温度相同,若两部分气体同时升高相同的温度,下列选项正确的是( )
如图,球形连通容器A置于水平面上,水平部分的水银将球内气体隔开,且V1>V2.开始时两边气体温度相同,若两部分气体同时升高相同的温度,下列选项正确的是( )
 如图,球形连通容器A置于水平面上,水平部分的水银将球内气体隔开,且V1>V2.开始时两边气体温度相同,若两部分气体同时升高相同的温度,下列选项正确的是( )
如图,球形连通容器A置于水平面上,水平部分的水银将球内气体隔开,且V1>V2.开始时两边气体温度相同,若两部分气体同时升高相同的温度,下列选项正确的是( )| A. | 水银柱将向左移动 | B. | 水银柱将向右移动 | ||
| C. | 地面对连通器A的摩擦力方向向左 | D. | 地面对连通器A无摩擦力作用 |
 木块和木板一起向右做匀速直线运动,木块的速度为5m/s,木板的速度为8m/s.在木块未离开木板时,分析木板和木块的受力情况.分别用点代替木板和木块画出它们的受力示意图.
木块和木板一起向右做匀速直线运动,木块的速度为5m/s,木板的速度为8m/s.在木块未离开木板时,分析木板和木块的受力情况.分别用点代替木板和木块画出它们的受力示意图.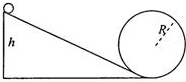 如图所示,一光滑斜面连接着一光滑竖直圆轨道,轨道半径为R,现有一质量为m的小球从h=3R的高度由静止滑下,试通过计算说明质点能否滑过轨道的最高点?如果能,求小球经过最高点时对轨道的压力大小.
如图所示,一光滑斜面连接着一光滑竖直圆轨道,轨道半径为R,现有一质量为m的小球从h=3R的高度由静止滑下,试通过计算说明质点能否滑过轨道的最高点?如果能,求小球经过最高点时对轨道的压力大小.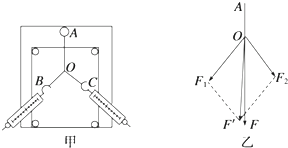
 (1)在做“探究力的合成方法”实验时,橡皮条的一端固定在木板上,用两个弹簧测力计把橡皮条的另一端拉到某一确定的O点,以下操作中错误的是ACD.
(1)在做“探究力的合成方法”实验时,橡皮条的一端固定在木板上,用两个弹簧测力计把橡皮条的另一端拉到某一确定的O点,以下操作中错误的是ACD.