题目内容
.图B-9中a1b1c1d1和a2b2c2d2为在同一竖直面内的金属导轨，处在垂直于纸面向里磁感应强度为B的匀强磁场中.导轨的a1b1段与a2b2段是竖直的，距离为l1；c1d1段与c1d2段也是竖直的，距离为l2.x1y1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆，质量分别为m1和m2，它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.F为作用于金属杆x1y1上的竖直向上的恒力.已知两杆运动到图示位置时，已匀速向上运动，求此时作用于两杆的重力的功率的大小和回路电阻上的热功率.
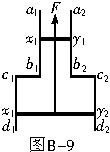
设杆向上运动的速度为v，因为杆的运动，两杆与导轨构成的回路的面积减少，磁通量也减少.根据法拉第电磁感应定律，回路中的感应电动势的大小
ε=B（l2-l1）v ①
回路中的电流 I=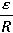
②
电流沿顺时针方向.两金属杆都要受到安培力作用，作用于杆x1y1的安培力为
f1=Bl1I ③
方向向上，作用于杆x2y2的安培力 f2=Bl2I ④
方向向下.当杆做匀速运动时，根据牛顿第二定律有
F-m2g-m2g+f2-f2=0 ⑤
解以上各式，得 I=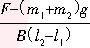
⑥
v=
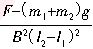R ⑦
作用于两杆的重力的功率的大小P重=（m1+m2）gv⑧
电阻上的热功率 P热=I2R⑨
由⑥、⑦、⑧、⑨式，可得
P重=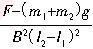
R（m1+m2）g
P热=［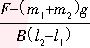
］2R
【试题分析】
练习册系列答案
相关题目