题目内容
1.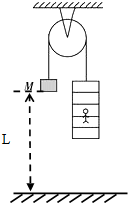 如图所示,一足够长细绳跨过装在天花板上的滑轮,细绳的一端悬挂一质量为M=55Kg的物体,距离地面L=6m,另一端悬挂一载人的梯子,人的质量为m=50Kg,系统处于平衡状态,不计摩擦及滑轮与细绳的质量,g=10m/s2.求:
如图所示,一足够长细绳跨过装在天花板上的滑轮,细绳的一端悬挂一质量为M=55Kg的物体,距离地面L=6m,另一端悬挂一载人的梯子,人的质量为m=50Kg,系统处于平衡状态,不计摩擦及滑轮与细绳的质量,g=10m/s2.求:(1)若人与梯子分离,不计分离时人对梯子的扰动,则分离后物体到达地面的时间为多少?
(2)要使天花板受力为零,人在梯子上应如何运动?
分析 (1)对系统研究,根据牛顿第二定律求出系统的加速度,结合位移时间公式求出分离后物体到达地面的时间.
(2)要使天花板受力为零,须使细绳中的拉力为零,物体M应做自由落体运动,故梯子应以加速度g向上匀加速运动.人对梯子的作用力向上,人应向下加速运动.
解答 解:(1)开始处于平衡,有:Mg=mg+m梯g,
解得m梯=5kg.
人与梯分离后,对系统研究,加速度a=$\frac{mg}{M+{m}_{梯}}=\frac{500}{55+5}=\frac{25}{3}m/{s}^{2}$,
根据L=$\frac{1}{2}a{t}^{2}$得,t=$\sqrt{\frac{2L}{a}}=\sqrt{\frac{2×6}{\frac{25}{3}}}s=1.2s$.
(2)设人与梯子之间的相互作用力为F,人向上的加速度为a.若使天花板受力为零,重物应处于完全失重,即下落加速度为g,对梯子运用牛顿第二定律:
F-m梯g=m梯g
对人运用牛顿第二定律:
F+mg=ma
又Mg=mg+m梯g,
解得a=$\frac{2M-m}{m}g=\frac{110-50}{50}×10=12m/{s}^{2}$,
故人以12m/s2的加速度向下加速运动,才能使天花板受力为零.
答:(1)分离后物体到达地面的时间为1.2s.
(2)要使天花板受力为零,人在梯子上以12m/s2的加速度向下加速运动.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,难度中等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.如图所示的位移(S)-时间(t)图象和速度(V)-时间(t)图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是( )


| A. | 图线1表示物体做曲线运动 | |
| B. | 两图象中,t2、t4时刻分别表示2、4开始反向运动 | |
| C. | v-t图象中0至t3时间内3和4的平均速度大小相等 | |
| D. | s-t图象中t1时刻v1>v2 |
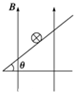
9. 如图所示,描述的是一做直线运动的物体其某一物理量随时间变化的图象,则下列关于此图象的说法中正确的是( )
如图所示,描述的是一做直线运动的物体其某一物理量随时间变化的图象,则下列关于此图象的说法中正确的是( )
 如图所示,描述的是一做直线运动的物体其某一物理量随时间变化的图象,则下列关于此图象的说法中正确的是( )
如图所示,描述的是一做直线运动的物体其某一物理量随时间变化的图象,则下列关于此图象的说法中正确的是( )| A. | 若y表示物体的位移,则反映物体做匀速直线运动 | |
| B. | 若y表示物体的位移,则反映物体做匀加速直线运动 | |
| C. | 若y表示物体的速度,则反映物体做匀速直线运动 | |
| D. | 若y表示物体的速度,则反映物体做匀加速直线运动 |
6.下列情况下,哪一个单摆的周期会变大( )
| A. | 用一个装满沙的轻漏斗做成单摆,在摆动时沙从漏斗中慢慢漏出 | |
| B. | 单摆振幅减为原来的一半 | |
| C. | 将摆由高山移到平地上 | |
| D. | 将摆由北极移到赤道 |
10.关于自由落体运动的加速度g,下列说法中正确的是( )
| A. | 重力加速度g是标量,只有大小没有方向,通常计算中g=9.8m/s2 | |
| B. | 同一地点、轻和重的物体的g值一样大 | |
| C. | g值在地球上任何地方都一样大 | |
| D. | 随纬度越高,g值越小 |
8. 从高出地面2m的位置竖直向上抛出一个球,它上升4m后回落,最后小球到达地面,如图所示,分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写表:
从高出地面2m的位置竖直向上抛出一个球,它上升4m后回落,最后小球到达地面,如图所示,分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写表:
 从高出地面2m的位置竖直向上抛出一个球,它上升4m后回落,最后小球到达地面,如图所示,分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写表:
从高出地面2m的位置竖直向上抛出一个球,它上升4m后回落,最后小球到达地面,如图所示,分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写表:| 坐标原点的设置 | 出发点的坐标 | 最高点的坐标 | 落地点的坐标 |
| 以地面为原点 | |||
| 以抛出点为原点 |
 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验: