题目内容
【题目】(1)质量为M 的火箭原来以速率为 v0飞行在太空中，现在突然喷出一份质量为m 的气体，喷出的气体相对于火箭的速率是 v，则喷气后火箭的速率为______；
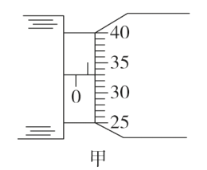
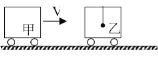
(2)如图所示，在光滑水平面上有甲、乙两辆完全相同的小车，质量都为M=1.0kg，乙车内用轻绳吊一质量为m=0.5kg 的小球。当乙车静止时，甲车以速度 v 与乙车相碰，若碰撞时间极短，且碰后两车连为一体，则碰后瞬间两车的共同速度为_______。当小球摆到最高点时，车的速度为_________；
(3)如果某物体作匀速圆周运动的动量大小为p，经过一段时间后其速度方向改变了θ角，它的动量变化的大小为_________；
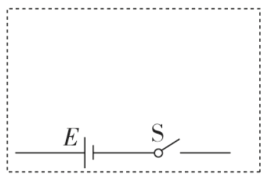
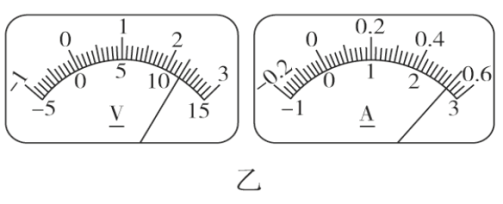
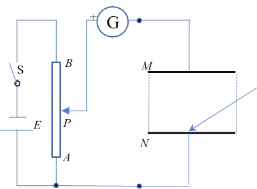
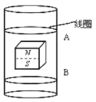
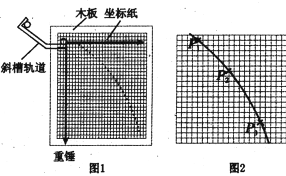
(4)用如图装置做探究碰撞中的不变量实验，下列说法正确的是（______）
A.在实验前，必须把长木板的一端垫高，使 A 能拖着纸带匀速下行
B.A、B 两辆小车的质量必须相等
C.A、B 碰撞后必须保证 A、B 以共同速度一起运动
D.小车 A 必须从紧靠打点计时器的位置无初速度释放
【答案】
AC
【解析】
(1)[1] 以火箭和喷出的气体为研究对象，以火箭飞行的方向为正方向，由动量守恒定律得：
解得：
(2)[2][3] 甲车与乙车相碰是在极短时间内发生的过程，两者（不包括乙车中的小球）动量守恒
Mv=2Mv1
解得：
此时乙车中悬挂的小球速度为零．然后在绳的拉力作用下，小球和甲、乙车的速度发生变化，三者组成的系统在水平方向上不受外力，水平方向上动量守恒．又根据运动情景分析可知，当小球运动到最高点的瞬间，车和球相对静止，设速度为v2，那么
解得：
(3)[4] 如果某物体作匀速圆周运动的动量大小为p，经过一段时间后其速度方向改变了θ角，根据矢量合成可知，两动量合成等腰三角形，根据几何关系可知，动量变化量大小为 。
(4)[5] A．根据动量守恒的条件可知，本实验需要平衡摩擦力，故在实验前，必须把长木板的一端垫高，使A能拖着纸带匀速下行，故A正确；
B． 本实验中对A、B两辆小车的质量无特殊要求，故B错误；
C． 为了得出动量守恒的表达式，A、B碰撞后必须保证A、B以共同速度一起运动，故C正确；
D． 碰撞前小车A应有速度，故小车A在手推动下开始运动，故D错误；
故选：AC。
