Question

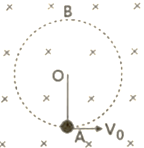
【题目】如图所示，一单边有界磁场的边界上有一粒子源，与水平方向成θ角的不同速率，向磁场中射入两个相同粒子1和2，粒子1经磁场偏转后从边界上A点出磁场，粒子2经磁场偏转后从边界上B点出磁场，OA=AB，则

A. 粒子1与粒子2的速度之比为1：2

B. 粒子1与粒子2的速度之比为1：4

C. 粒子1与粒子2在磁场中运动的时间之比为1：1

D. 粒子1与粒子2在磁场中运动的时间之比为1：2

Answer 1

【答案】AC

【解析】

根据几何关系：入射点速度的垂线与入射点和出射点连线的中垂线的交点为圆心画出两个粒子的运动轨迹图像；由粒子在磁场中做匀速圆周运动，洛仑兹力提供向心力，求出粒子在磁场中的运动半径表达式，结合图像中的几何关系确定两个粒子的速度关系；根据粒子在磁场中做匀速圆周运动的周期公式：，确定两个粒子的运动周期，再结合粒子在磁场中转过的圆心角，确定粒子在磁场中的运动时间；

AB、粒子进入磁场后速度的垂线与OA的垂直平分线的交点为粒子1在磁场中的轨迹圆的圆心；同理，粒子进入磁场后速度的垂线与OB的垂直平分线的交点为粒子2在磁场中的轨迹圆的圆心；由几何关系可知,两个粒子在磁场中做圆周运动的半径之比为，由可知，粒子1与粒子2的速度之比为1:2，故A正确，B错误；

CD、由于粒子在磁场中做圆周运动的，周期均为，且两粒子在磁场中做圆周运动的轨迹所对的圆心角相同，根据公式，两个粒子在磁场中运动的时间相等，故C正确，D错误；

故选AC。