Question

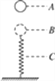
【题目】一长木板置于光滑水平地面上，木板左端放置一小物块，在木板右方有一墙壁，如图所示．t=0时刻开始，小物块与木板一起以共同速度向右运动，直至木板与墙壁碰撞（碰撞时间极短）．碰撞前后木板速度大小不变，方向相反；运动过程中小物块始终未离开木板．已知小物块与木板间的动摩擦因素为0.4，木板的质量是小物块质量的1.5倍，重力加速度大小g取10m/s2．求

（1）木板和木块的最终速度v；

（2）木板的最小长度L；

Answer 1

【答案】（1）0.8m/s；（2）4.8m

【解析】（1）碰撞前小物块与木板共同速度为v0=4m/s，碰撞后木板速度水平向左，大小也是v0=4m/s，设小物块的质量为m，则木板的质量为1.5m，从和墙碰后到二者共速，取向左的方向为正方向，根据定律守恒定律有：
1.5mv0-mv0=（1.5m+m）v，
解得：v=0.8m/s．

（2）由功能关系得：

解得：L=4.8m．