题目内容
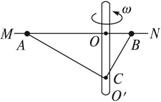
如图5-7-9所示，OO′为竖直转轴，MN为固定在OO′的水平光滑杆，有两个质量相同的金属球A、B套在水平杆上，AC、BC为抗拉能力相同的两根细线，C端固定在转轴OO′上.当线拉直时，A、B两球的转动的半径之比恒为2∶1，当转轴角速度增大时（ ）
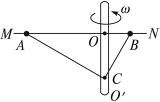
图5-7-9
A.AC线先断 B.BC线先断
C.两线同时断 D.不能确定哪段线先断
A
解析:
两球角速度相同，半径之比为2∶1，只要能找到它们所需的向心力与绳子承担的拉力之间的关系，即可进行分析比较.
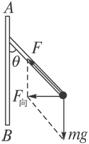
每个小球均受三个力的作用：重力、杆的弹力（竖直向上）和绳子的拉力（设拉力为F，与水平杆夹角为
）.其中拉力的水平分量
提供小球在水平面内做匀速圆周运动的向心力，
.由数学知识，
，二式联立得
.由于A、B两球质量m相同，套在同一水平杆MN上，角速度ω时刻相同，当两根细线拉直时，转动的半径之比恒为2∶1，即rA>rB，因此由上式可知，细线所受拉力F的大小只与半径r有关，r越大，受力越大.即连接A球的AC线受力大，而AC、BC两根细线抗拉能力又相同，故当角速度ω增大时，AC线先断，选项A正确.
练习册系列答案
相关题目
