题目内容
19.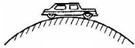 一辆汽车以15m/s的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,
一辆汽车以15m/s的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,(1)这座拱桥的半径是多少m?
(2)若要使汽车过桥顶时对桥面无压力,则汽车过桥顶时的速度大小至少是多少m/s.
分析 (1)在最高点,根据径向的合力提供向心力,通过牛顿第二定律求出拱桥的半径.
(2)当压力为零时,靠重力提供向心力,根据牛顿第二定律求出汽车在桥顶的速度大小.
解答 解:(1)根据mg-N=$m\frac{{v}^{2}}{R}$,N=$\frac{1}{2}mg$,
解得R=$\frac{{v}^{2}}{\frac{1}{2}g}=\frac{225}{5}m=45m$.
(2)当汽车对桥顶压力为零时,根据牛顿第二定律得,
$mg=m\frac{{v}^{2}}{R}$,
解得v=$\sqrt{gR}=\sqrt{10×45}m/s=15\sqrt{2}m/s$.
答:(1)这座桥的半径为45m.
(2)汽车过桥顶时的速度大小至少是$15\sqrt{2}$m/s.
点评 解决本题的关键知道汽车在桥顶向心力的来源,结合牛顿第二定律进行求解,知道压力为零时,靠重力提供向心力,基础题.

练习册系列答案
相关题目
10.如图所示,在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动,物体相对桶壁静止.则( )


| A. | 物体受到3个力的作用 | B. | 物体所受向心力是重力提供的 | ||
| C. | 物体所受向心力是弹力提供的 | D. | 物体所受向心力是静摩擦力提供 |
14.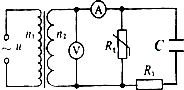 如图理想变压器,原、副线圈的匝数比为2:1,原线圈接有交流电压u=220sin100t V;图中电压表和电流表均为理想交流电表,Rt为负温度系数的热敏电阻(即当温度升高时,阻值减小),R1为定值电阻,C为电容器.下列说法正确的是( )
如图理想变压器,原、副线圈的匝数比为2:1,原线圈接有交流电压u=220sin100t V;图中电压表和电流表均为理想交流电表,Rt为负温度系数的热敏电阻(即当温度升高时,阻值减小),R1为定值电阻,C为电容器.下列说法正确的是( )
 如图理想变压器,原、副线圈的匝数比为2:1,原线圈接有交流电压u=220sin100t V;图中电压表和电流表均为理想交流电表,Rt为负温度系数的热敏电阻(即当温度升高时,阻值减小),R1为定值电阻,C为电容器.下列说法正确的是( )
如图理想变压器,原、副线圈的匝数比为2:1,原线圈接有交流电压u=220sin100t V;图中电压表和电流表均为理想交流电表,Rt为负温度系数的热敏电阻(即当温度升高时,阻值减小),R1为定值电阻,C为电容器.下列说法正确的是( )| A. | 交流电的频率为100 Hz | |
| B. | 变压器输入、输出功率之比为2:1 | |
| C. | 电压表示数是110V,通过R1的电流始终为零 | |
| D. | 当Rt处温度升高时,电压表示数不变,电流表示数变大 |
4.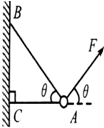 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )| A. | 4$\sqrt{3}$N | B. | 8$\sqrt{3}$N | C. | 12$\sqrt{3}$N | D. | 16$\sqrt{3}$N |
8.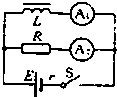 带铁心的电感线圈,其直流电阻与电阻R的阻值相同,A1和A2是两个完全相同的电流表,它们组成如图所示电路,则下列说法中正确的是( )
带铁心的电感线圈,其直流电阻与电阻R的阻值相同,A1和A2是两个完全相同的电流表,它们组成如图所示电路,则下列说法中正确的是( )
 带铁心的电感线圈,其直流电阻与电阻R的阻值相同,A1和A2是两个完全相同的电流表,它们组成如图所示电路,则下列说法中正确的是( )
带铁心的电感线圈,其直流电阻与电阻R的阻值相同,A1和A2是两个完全相同的电流表,它们组成如图所示电路,则下列说法中正确的是( )| A. | 闭合S的瞬时,电流表A1的示数小于A2,指针偏转方向与A2相同 | |
| B. | 闭合S的瞬时,电流表A1的示数等于A2,指针偏转方向与A2相反 | |
| C. | 断开S的瞬时,电流表A1的示数大于A2,指针偏转方向与A2相反 | |
| D. | 断开S的瞬时,电流表A1的示数等于A2,指针偏转方向与A2相同 |
9.在电能的输送过程中,若输送的电功率一定、输电线电阻一定时,此时在输电线上损失的电功率为P,若升压变压器副线圈匝数变为原来的n倍,则输电线上损失的功率为( )
| A. | nP | B. | n2P | C. | $\frac{P}{n}$ | D. | $\frac{P}{n^2}$ |
 如图所示,水平传送带AB的长度L=3.75m,皮带轮的半径R=0.1m.现有一个小物体(可视为质点)以水平速度v0从A点滑上传送带,物体与传送带间动摩擦因素μ=0.2,传送带上表面距地面高度h=5m,g取10m/s2,试讨论以下问题:
如图所示,水平传送带AB的长度L=3.75m,皮带轮的半径R=0.1m.现有一个小物体(可视为质点)以水平速度v0从A点滑上传送带,物体与传送带间动摩擦因素μ=0.2,传送带上表面距地面高度h=5m,g取10m/s2,试讨论以下问题:
 小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳恰好断掉,球飞行水平距离d后落地,如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为$\frac{3}{4}d$,重力加速度为g.忽略手的运动半径和空气阻力.
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳恰好断掉,球飞行水平距离d后落地,如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为$\frac{3}{4}d$,重力加速度为g.忽略手的运动半径和空气阻力.