题目内容
13.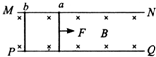 如图所示,MN、PQ为水平面内平行放置且足够长的固定金属导轨,导轨间距为L,导轨处于方向竖直向下、磁感应强度大小为B的匀强磁场中.两根完全相同的金属棒a、b垂直MN、PQ放置在导轨上,长均为L、质量均为m、电阻均为R,棒与导轨电接触良好.现对a施加水平向右的恒力F,a由静止开始向右运动,移动距离x时速度为v,此时b开始运动.设最大静摩擦力与滑动摩擦力大小相等,导轨电阻不计,求:
如图所示,MN、PQ为水平面内平行放置且足够长的固定金属导轨,导轨间距为L,导轨处于方向竖直向下、磁感应强度大小为B的匀强磁场中.两根完全相同的金属棒a、b垂直MN、PQ放置在导轨上,长均为L、质量均为m、电阻均为R,棒与导轨电接触良好.现对a施加水平向右的恒力F,a由静止开始向右运动,移动距离x时速度为v,此时b开始运动.设最大静摩擦力与滑动摩擦力大小相等,导轨电阻不计,求:(1)b开始运动时,回路的电功率P:
(2)a刚拉动时的加速度a0;
(3)在a移动距离x的过程中,b中产生的电热Qb.
分析 (1)根据E=BLv、I=$\frac{E}{2R}$、P=IE结合求解回路的电功率P.
(2)b刚开始运动时所受的滑动摩擦力等于安培力,列式可求得滑动摩擦力.a、b受到的滑动摩擦力相同,即可根据牛顿第二定律求解加速度.
(3)根据功能关系求解b中产生的焦耳热Qb.
解答 解:(1)设b开始运动时,a产生的电势能为E,则:
E=BLv
回路电流为:I=$\frac{E}{2R}$
电功率 P=IE
联立解得回路的电功率为:P=$\frac{{B}^{2}{L}^{2}{v}^{2}}{2R}$
(2)b刚拉动时,f滑=F安=BIL
a、b受到的滑动摩擦力相同,则a刚拉动时速度为零,没有感应电流,不受安培力,由牛顿第二定律有:
F-f滑=ma0
解得:a0=$\frac{F}{m}$-$\frac{{B}^{2}{L}^{2}v}{2mR}$
(3)对a杆由功能关系:$Fx-μmgx=\frac{1}{2}m{v^2}+Q$
对b杆:BIL=μmg
由能量分配关系:$\frac{Q_b}{Q}=\frac{R}{2R}$
解得:${Q_b}=\frac{1}{2}Fx-\frac{{{B^2}{L^2}xv}}{4R}-\frac{1}{4}m{v^2}$
答:(1)b开始运动时,回路的电功率P是$\frac{{B}^{2}{L}^{2}{v}^{2}}{2R}$;
(2)a刚拉动时的加速度a0是$\frac{F}{m}$-$\frac{{B}^{2}{L}^{2}v}{2mR}$;
(3)在a移动距离x的过程中,通过回路的电荷量q和b中产生的焦耳热Qb是$\frac{1}{2}Fx-\frac{{B}^{2}{L}^{2}xv}{4R}-\frac{1}{4}m{v}^{2}$.
点评 本题比较简单考查了电磁感应与电路、力学知识的结合,解决这类问题的关键是正确分析外电路的结构,熟练推导安培力的表达式和感应电荷量表达式.


| A. | 由波形图可知该波的波长 | B. | 由波形图可知该波的周期 | ||
| C. | 经$\frac{1}{4}$周期后质点P运动到Q点 | D. | 经$\frac{1}{4}$周期后质点R的速度变为零 |
| A. | 只要速度的大小相同,所受的洛仑兹力的大小就相同 | |
| B. | 运动电荷在磁感应强度不为零的地方,一定受到洛仑兹力的作用 | |
| C. | 只有粒子垂直射入磁场,粒子才受到洛仑兹力的作用 | |
| D. | 当粒子垂直射入磁场时,当两粒子的电量相同,速度大小相同,它们所处的磁场磁感应强度相同,则它们所受的洛仑兹力大小相等 |
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 分子间引力总是随着分子间的距离减小而减小 | |
| C. | 水的饱和汽压随温度的升高而增大 | |
| D. | 分子热运动越剧烈,物体内每个分子的动能越大 | |
| E. | 物体的内能跟物体的温度和体积有关 | |
| F. | 对某物体做功,必定会使该物体的内能增加 | |
| G. | 可以从单一热源吸收热量,使之完全变为功 | |
| H. | 不可能使热量从低温物体传向高温物体 | |
| I. | 功转变为热的实际宏观过程是不可逆过程 | |
| J. | 相对湿度是指空气中实际所含水蒸汽压强和同温度下饱和水蒸汽压强的百分比值 |
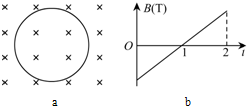 一个环形线圈放在磁场中,如图a所示,以磁感线垂直于线圈平面向外的方向为正方向,若磁感强度B随时间t的变化的关系如图b,那么在第2秒内线圈中的感应电流的大小和方向是( )
一个环形线圈放在磁场中,如图a所示,以磁感线垂直于线圈平面向外的方向为正方向,若磁感强度B随时间t的变化的关系如图b,那么在第2秒内线圈中的感应电流的大小和方向是( )| A. | 大小恒定,顺时针方向 | B. | 逐渐减小,顺时针方向 | ||
| C. | 大小恒定,逆时针方向 | D. | 逐渐增加,逆时针方向 |
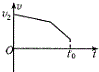
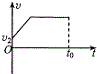
 如图所示,倾斜传送带以速度v1顺时针匀速运动,t=0时刻小物体从底端以速度v2冲上传送带,t=t0时刻离开传送带,下列描述小物体的速度随时间变化的图象可能正确的是( )
如图所示,倾斜传送带以速度v1顺时针匀速运动,t=0时刻小物体从底端以速度v2冲上传送带,t=t0时刻离开传送带,下列描述小物体的速度随时间变化的图象可能正确的是( )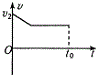
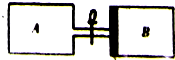 如图所示,导热材料制成的截面积相等,长度均为45cm的气缸A、B通过带有阀门的管道连接.初始时阀门关闭,厚度不计的光滑活塞C位于B内左侧,在A内充满压强PA=2.8×105Pa的理想气体,B内充满压强PB=1.4×105 Pa的同种理想气体,忽略连接气缸的管道体积,室温不变.现打开阀门,求最终平衡时活塞向右移动的距离.
如图所示,导热材料制成的截面积相等,长度均为45cm的气缸A、B通过带有阀门的管道连接.初始时阀门关闭,厚度不计的光滑活塞C位于B内左侧,在A内充满压强PA=2.8×105Pa的理想气体,B内充满压强PB=1.4×105 Pa的同种理想气体,忽略连接气缸的管道体积,室温不变.现打开阀门,求最终平衡时活塞向右移动的距离.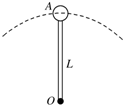 长L=0.5m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个物体A.A的质量为m=2kg,当A通过最高点时,如图所示,求在下列两种情况下杆对小球的力.(g=10m/s2)
长L=0.5m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个物体A.A的质量为m=2kg,当A通过最高点时,如图所示,求在下列两种情况下杆对小球的力.(g=10m/s2)