题目内容
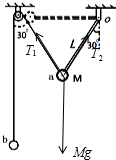
 如图所示,小球a的质量为M,被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点,同时又通过绳跨过光滑定滑轮与另一个小球b相连,O轴与左边定滑轮等高,且它们之间的距离等于轻杆长L,整个装置平衡时杆和绳与竖直方向的夹角均为30°,小球b的质量m为1kg.
如图所示,小球a的质量为M,被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点,同时又通过绳跨过光滑定滑轮与另一个小球b相连,O轴与左边定滑轮等高,且它们之间的距离等于轻杆长L,整个装置平衡时杆和绳与竖直方向的夹角均为30°,小球b的质量m为1kg.(1)求小球a的质量M等于多少kg?
(2)若将小球a拉水平位置(杆呈水平状态)开始释放,不计摩擦,重力加速度g取10m/s2,竖直绳足够长,求当杆转动到竖直位置时,小球b的速度大小.
分析:(1)小球a受力平衡,根据共点力平衡得出M和m的关系即可;
(2)小球a从水平位置运动到竖直位置,a、b两球组成的系统机械能守恒,a球运动到最低点,a球沿绳子方向上的分速度等于b的速度,根据系统机械能守恒求出小球b的速度.
(2)小球a从水平位置运动到竖直位置,a、b两球组成的系统机械能守恒,a球运动到最低点,a球沿绳子方向上的分速度等于b的速度,根据系统机械能守恒求出小球b的速度.
解答:解:对小球a受力分析,受重力Mg、细线的拉力(等于mg)、杆的拉力,如图所示
根据平衡条件,有:
T1sin30°=T2sin30°
T1cos30°+T2cos30°-Mg=0
其中:T1=mg=10N
联立解得:T2=10
N=17.3N
故M=1.73kg
(2)当a球转到竖直位置时,a球下落高度为L,绳与竖直方面成45°角,b球上升的高度为h=
L
设此时a球、b球的速度分别为va,vb
有va=
vb
在整个运动过程中,由机械能守恒.
MgL-mg?
L=
M
+
m
由以上3式得出b球的速度
vb=
=0.84m/s
答:(1)小球a的质量M等于1.73kg;
(2)小球b的速度为0.84m/s.

根据平衡条件,有:
T1sin30°=T2sin30°
T1cos30°+T2cos30°-Mg=0
其中:T1=mg=10N
联立解得:T2=10
| 3 |
故M=1.73kg
(2)当a球转到竖直位置时,a球下落高度为L,绳与竖直方面成45°角,b球上升的高度为h=
| 2 |
设此时a球、b球的速度分别为va,vb
有va=
| 2 |
在整个运动过程中,由机械能守恒.
MgL-mg?
| 2 |
| 1 |
| 2 |
| v | 2 a |
| 1 |
| 2 |
| v | 2 b |
由以上3式得出b球的速度
vb=
|
答:(1)小球a的质量M等于1.73kg;
(2)小球b的速度为0.84m/s.
点评:解决本题的关键知道小球b在沿绳子方向上的分速度等于a的速度,对系统研究,运用机械能守恒定律进行求解.

练习册系列答案
相关题目
 (2012?黄埔区模拟)如图所示,小球a的质量为M,被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点,同时又通过绳跨过光滑定滑轮与另一个小球b相连,整个装置平衡时杆和绳与竖直方向的夹角均为30°.若将小球a拉水平位置(杆呈水平状态)开始释放,不计摩擦,重力加速度g取10m/s2,竖直绳足够长,求当杆转动到竖直位置时,小球b的速度大小.
(2012?黄埔区模拟)如图所示,小球a的质量为M,被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点,同时又通过绳跨过光滑定滑轮与另一个小球b相连,整个装置平衡时杆和绳与竖直方向的夹角均为30°.若将小球a拉水平位置(杆呈水平状态)开始释放,不计摩擦,重力加速度g取10m/s2,竖直绳足够长,求当杆转动到竖直位置时,小球b的速度大小.
