题目内容
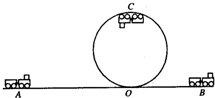 为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验:让车在P=35kW的恒定功率牵引下,从A点由静止开始沿水平轨道做加速直线运动,经20s到O点时关闭发动机让其冲上半径R=10m的圆形轨道,沿内侧滑行,通过最高点C时的速度恰好是车不脱离轨道的临界速度,最后在右侧的水平轨道滑行至B点停止,设车的总质量m=2t,车在左右水平轨道上所受阻力均是车重的0.1倍,在圆形轨道上所受阻力不计,计算时过山车可看作质点,g取10m/s2.在这次试车中
为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验:让车在P=35kW的恒定功率牵引下,从A点由静止开始沿水平轨道做加速直线运动,经20s到O点时关闭发动机让其冲上半径R=10m的圆形轨道,沿内侧滑行,通过最高点C时的速度恰好是车不脱离轨道的临界速度,最后在右侧的水平轨道滑行至B点停止,设车的总质量m=2t,车在左右水平轨道上所受阻力均是车重的0.1倍,在圆形轨道上所受阻力不计,计算时过山车可看作质点,g取10m/s2.在这次试车中(1)A、O之间的距离s1为多大?
(2)车在O点时对轨道压力多大?
分析:(1)根据车在最高点受力分析,结合牛顿第二定律与向心力表达式,可求出最高点的速度,并由机械能守恒定律与动能定理相综合,即可求解;
(2)根据牛顿第二定律,结合在O点受力分析,即可求出轨道对车的支持力,再由牛顿第三定律,即可求解.
(2)根据牛顿第二定律,结合在O点受力分析,即可求出轨道对车的支持力,再由牛顿第三定律,即可求解.
解答:解:(1)设过山车在最高点C的速度vc
由 mg=m
则有vc=
代入数据,解得:vc=10m/s
由O到C点机械能守恒,以O点为零势能,
则有:
m
=mg?2R+
m
代入数据,解得:v0=10
m/s
对A到O点过程中,运用动能定理,可得:Pt-kmgS1=
m
代入数据,解得:S1=100m
(2)设在O点轨道对车支持力N,则有:N-mg=m
则N=mg+m
代入数据,解得:N=1.2×105N
根据牛顿第三定律,车对轨道压力为1.2×105N.
答:(1)A、O之间的距离s1为100m;
(2)车在O点时对轨道压力1.2×105N.
由 mg=m
| ||
| R |
则有vc=
| gR |
代入数据,解得:vc=10m/s
由O到C点机械能守恒,以O点为零势能,
则有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 c |
代入数据,解得:v0=10
| 5 |
对A到O点过程中,运用动能定理,可得:Pt-kmgS1=
| 1 |
| 2 |
| v | 2 0 |
代入数据,解得:S1=100m
(2)设在O点轨道对车支持力N,则有:N-mg=m
| ||
| R |
则N=mg+m
| ||
| R |
代入数据,解得:N=1.2×105N
根据牛顿第三定律,车对轨道压力为1.2×105N.
答:(1)A、O之间的距离s1为100m;
(2)车在O点时对轨道压力1.2×105N.
点评:考查受力分析的思路,掌握牛顿第二、三定律,及机械能守恒定律与动能定理的应用,知道向心力表达式,注意机械能守恒条件判定.

练习册系列答案
相关题目
结合下图,关于机械能守恒说法正确的是:(忽略空气阻力)( )
A、 将箭搭在弦上,拉弓的整个过程,弓和箭组成的系统机械能守恒 将箭搭在弦上,拉弓的整个过程,弓和箭组成的系统机械能守恒 | B、 在动力作用下从轨道上缓慢上行的过山车,过山车机械能守恒 在动力作用下从轨道上缓慢上行的过山车,过山车机械能守恒 | C、 在一根细线的中央悬挂着一物体,双手拉着细线慢慢分开的过程中,物体机械能守恒 在一根细线的中央悬挂着一物体,双手拉着细线慢慢分开的过程中,物体机械能守恒 | D、 将内有弹簧的圆珠笔的笔帽抵在桌面,放手后圆珠笔弹起的过程,笔的机械能守恒 将内有弹簧的圆珠笔的笔帽抵在桌面,放手后圆珠笔弹起的过程,笔的机械能守恒 |

 为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验:
为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验: