题目内容
20. 如图所示,在水平光滑的xOy平面内,存在一个竖直向下的稳定磁场,已知磁场的磁感应强度B在y轴方向按B=B0+ky规律逐渐增大,k为已知常量.在坐标原点处有一个正方形的闭合导线框,在水平平面内线框以沿x轴正方向的初速度v0开始运动,同时受到一个沿y轴正方向的水平恒力F作用,线框运动过程中不发生转动,已知闭合线框的边长为a,质量为m,电阻为R,试求:
如图所示,在水平光滑的xOy平面内,存在一个竖直向下的稳定磁场,已知磁场的磁感应强度B在y轴方向按B=B0+ky规律逐渐增大,k为已知常量.在坐标原点处有一个正方形的闭合导线框,在水平平面内线框以沿x轴正方向的初速度v0开始运动,同时受到一个沿y轴正方向的水平恒力F作用,线框运动过程中不发生转动,已知闭合线框的边长为a,质量为m,电阻为R,试求:(1)线框运动足够长时间后速度的大小;
(2)闭合线框的最大发热功率.
分析 (1)线框运动过程中左右两边切割磁感线产生的感应电动势抵消,回路产生的感应电动势是上下两边产生的感应电动势之差,左右两边受到的安培力合力为零,线框在水平方向做匀速直线运动,线框在竖直方向先做加速运动,足够长时间后,线框所受合力为零,在竖直方向做匀速直线运动,应用平衡条件求出竖直方向的速度,然后求出线框的速度.
(2)当线框受到最大时,产生的感应电动势最大,线框发热功率最大,应用电功率公式可以求出最大发热功率.
解答 解:(1)时间足够长后,线框在竖直方向上最匀速直线运动,
线框产生的感应电动势:E=E上-E下=B上avy-B下avy=(B0+ky+ka)avy-(B0+ky)avy=ka2vy,
感应电流:I=$\frac{E}{R}$=$\frac{k{a}^{2}{v}_{y}}{R}$,
安培力:F安培=BIa=$\frac{Bk{a}^{3}{v}_{y}}{R}$,
方向做匀速直线运动,
由平衡条件得:F+F安培下=F安培上,
F=F安培上-F安培下=$\frac{({B}_{上}-{B}_{下})k{a}^{3}{v}_{y}}{R}$=$\frac{ka×k{a}^{3}{v}_{y}}{R}$=$\frac{{k}^{2}{a}^{4}{v}_{y}}{R}$,
解得,竖直分速度:vy=$\frac{FR}{{k}^{2}{a}^{4}}$,
线框的速度大小:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{v}_{0}^{2}+\frac{{F}^{2}{R}^{2}}{{k}^{4}{a}^{8}}}$;
(2)线框的最大感应电动势:
E最大=ka2vy=$\frac{FR}{k{a}^{2}}$,
闭合线框的最大发热功率:
P=$\frac{{E}_{最大}^{2}}{R}$=$\frac{{F}^{2}R}{{k}^{2}{a}^{4}}$;
答:(1)线框运动足够长时间后速度的大小为$\sqrt{{v}_{0}^{2}+\frac{{F}^{2}{R}^{2}}{{k}^{4}{a}^{8}}}$;
(2)闭合线框的最大发热功率为$\frac{{F}^{2}R}{{k}^{2}{a}^{4}}$.
点评 本题中磁场是非匀强磁场,线框四边都切割磁感线,左右两边电动势抵消,所受的安培力也抵消,根据E=BLv分别得到上下两边的电动势,再求总电动势,应用安培力公式、平衡条件与电功率公式可以解题.

 名校课堂系列答案
名校课堂系列答案 如图所示,灯泡A、B与固定电阻的阻值均为R,L是带铁芯的理想线圈,电源的内阻不计.开关S1、S2均闭合且电路达到稳定.已知电路中的各种元件均在安全范围之内.下列判断中正确的是( )
如图所示,灯泡A、B与固定电阻的阻值均为R,L是带铁芯的理想线圈,电源的内阻不计.开关S1、S2均闭合且电路达到稳定.已知电路中的各种元件均在安全范围之内.下列判断中正确的是( )| A. | 灯泡A中有电流通过,方向为a→b | |
| B. | 将S1断开的瞬间,灯泡A、B同时熄灭 | |
| C. | 将S1断开的瞬间,通过灯泡A的电流最大值要比原来通过灯泡B的电流大 | |
| D. | 将S2断开,电路达到稳定,灯泡A、B的亮度相同 |
| A. | 所有地球同步卫星一定在赤道上空 | |
| B. | 不同的地球同步卫星,离地高度不同 | |
| C. | 所有地球同步卫星的向心加速度大小和方向一定相同 | |
| D. | 所有地球同步卫星受的向心力大小一定相等 |
| A. | 气体的密度增大 | B. | 气体的压强增大 | ||
| C. | 气体分子的平均动能减小 | D. | 气体分子的平均动能增大 |
| A. | 电场强度大的地方电势一定高 | |
| B. | 电势为零的地方场强也一定为零 | |
| C. | 沿电场线方向电势越来越低,场强越来越小 | |
| D. | 场强和电势都跟电场中是否存在试探电荷无关 |
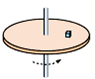 如图所示,一个水平匀质圆盘绕垂直于盘面的固定对称轴匀速转动,角速度是4rad/s,盘面上离转轴距离0.1m处有一质量为0.1kg的小物体能随盘一起转动.求:
如图所示,一个水平匀质圆盘绕垂直于盘面的固定对称轴匀速转动,角速度是4rad/s,盘面上离转轴距离0.1m处有一质量为0.1kg的小物体能随盘一起转动.求: 如图所示,光华斜面倾角为30°,斜面底端固定一个轻质弹簧,劲度系数为50N/m,弹簧上端与质量为1kg的甲物块相连,静止时甲物块在O点处,弹簧的弹性势能为0.25J,从距O点1.6m处的A点由静止释放质量也是1kg的乙物块,乙物块运动到O点处与甲物块相碰,然后一起压缩弹簧(甲、乙两物块不粘连,均可看作质点),经0.1s后两物块分离,求从两物块相碰到分离过程中弹簧弹力的冲量.(取重力加速度g=10m/s2,$\sqrt{3.25}$=1.8)
如图所示,光华斜面倾角为30°,斜面底端固定一个轻质弹簧,劲度系数为50N/m,弹簧上端与质量为1kg的甲物块相连,静止时甲物块在O点处,弹簧的弹性势能为0.25J,从距O点1.6m处的A点由静止释放质量也是1kg的乙物块,乙物块运动到O点处与甲物块相碰,然后一起压缩弹簧(甲、乙两物块不粘连,均可看作质点),经0.1s后两物块分离,求从两物块相碰到分离过程中弹簧弹力的冲量.(取重力加速度g=10m/s2,$\sqrt{3.25}$=1.8)