题目内容
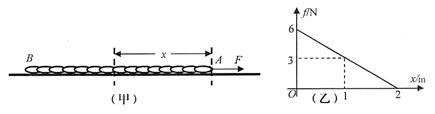
 一根质量分布均匀的长绳AB,在水平外力F的作用下,沿光滑水平面做直线运动,如图甲所示.绳内距A端S处的张力FT与S的关系如图乙所示,由图可知( )
一根质量分布均匀的长绳AB,在水平外力F的作用下,沿光滑水平面做直线运动,如图甲所示.绳内距A端S处的张力FT与S的关系如图乙所示,由图可知( )分析:绳子均匀分布,且作为一整体,其每一部分的加速度都应该是相同的,因此离作用点越近的地方力应该越大(要拖动后面的部分),在末尾处受力为0,根据图象结合牛顿第二定律即可求解.
解答:解:A、图中得知:既然距离A端为0时F最大,那么A端就应该是作用点,此时F=6N,所以水平外力F=6 N,故A正确;
B、设绳子运动的加速度为a,根据牛顿第二定律得:FA=ma,知道只FA无法求解质量,也无法求解加速度,故BD错误;
C、由图象可知x=2m 时张力为0 即B端距A端距离为2m,故C正确;
故选AC
B、设绳子运动的加速度为a,根据牛顿第二定律得:FA=ma,知道只FA无法求解质量,也无法求解加速度,故BD错误;
C、由图象可知x=2m 时张力为0 即B端距A端距离为2m,故C正确;
故选AC
点评:本题主要考查了同学们读图的能力,要求同学们能根据图象得出有效信息并结合牛顿第二定律解题,难度适中.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
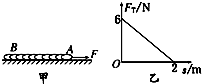
 2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力)
2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力)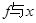 的关系如图乙所示,利用图象和题中的已知数据,求:
的关系如图乙所示,利用图象和题中的已知数据,求:
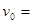 2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力)
2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力)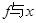 的关系如图乙所示,利用图象和题中的已知数据,求:
的关系如图乙所示,利用图象和题中的已知数据,求: