题目内容
10. 如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;$\overline{QN}$=2d、$\overline{PN}$=3d,离子重力不计.
如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;$\overline{QN}$=2d、$\overline{PN}$=3d,离子重力不计.(1)求圆弧虚线对应的半径R的大小;
(2)若离子恰好能打在NQ的中点上,求矩形区域QNCD内匀强电场场强E的值;
(3)若撤去矩形区域QNCD内的匀强电场,换为垂直纸面向里的匀强磁场,要求离子能最终打在QN上,求磁场磁感应强度B的取值范围.
分析 (1)离子在加速电场中加速时,电场力做功,动能增加,根据动能定理列出方程;粒子进入静电分析器,靠电场力提供向心力,结合牛顿第二定律列出方程,即可求出圆弧虚线对应的半径R的大小.
(2)离子进入矩形区域的有界匀强电场后做类平抛运动,将其进行正交分解,由牛顿第二定律和运动学公式结合,可求解场强E0的值.
(3)离子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律得到轨迹半径.画出粒子刚好打在QN上的临界轨迹,由几何关系求出临界的轨迹半径,即可求得B的范围.
解答 解:(1)离子在加速电场中加速,根据动能定理有:qU=$\frac{1}{2}$mv2-0,
离子在辐向电场中做匀速圆周运动,电场力提供向心力,根据牛顿第二定律有:qE0=m$\frac{{v}^{2}}{R}$,
解得:R=$\frac{2U}{{E}_{0}}$;
(2)离子做类平抛运动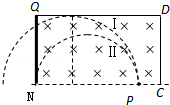
水平方向:d=vt,
竖直方向:3d=$\frac{1}{2}$at2,
由牛顿第二定律得:qE=ma,
解得:E=$\frac{3UR}{2d}$;
(3)离子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有:qvB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{1}{B}$$\sqrt{\frac{mER}{q}}$,
离子能打在QF上,则没有从DQ边出去也没有从PF边出去,离子运动的边界如图中Ⅰ和Ⅱ.
由几何关系知,离子能打在QF上,必须满足:$\frac{3}{2}$d<r≤2d,
则有:$\frac{1}{2d}$$\sqrt{\frac{mER}{q}}$≤B<$\frac{2}{3d}$$\sqrt{\frac{mER}{q}}$;
答:(1)圆弧虚线对应的半径R的大小为$\frac{2U}{{E}_{0}}$;
(2)若离子恰好能打在NQ的中点上,矩形区域QNCD内匀强电场场强E的值为$\frac{3UR}{2d}$;
(3)若撤去矩形区域QNCD内的匀强电场,换为垂直纸面向里的匀强磁场,要求离子能最终打在QN上,磁场磁感应强度B的取值范围是$\frac{1}{2d}$$\sqrt{\frac{mER}{q}}$≤B<$\frac{2}{3d}$$\sqrt{\frac{mER}{q}}$.
点评 对于带电粒子在电场中加速过程,往往运用动能定理研究加速电压与速度的关系;对于电场中偏转问题,运动的分解是常用方法.磁场中的匀速圆周运动,要知道洛伦兹力充当向心力,画出轨迹是解答的关键,同时注意粒子在静电分析器中电场力不做功.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
| A. | 绳的拉力不断增大 | B. | 绳的拉力不变 | ||
| C. | 船所受浮力不断增大 | D. | 拉绳的速度不断减小 |
| A. | 卫星A的线速度大于第一宇宙速度 | |
| B. | 卫星A的向心加速度是地球表面重力加速度的$\frac{4}{49}$倍 | |
| C. | 同步卫星B的向心加速度为地球表面赤道上物体随地球自转向心加速度的$\frac{1}{49}$倍 | |
| D. | 卫星B的周期小于卫星A的周期 |
 图示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )
图示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )| A. | 金属框内感应电流方向先顺时针再逆时针 | |
| B. | 金属框内感应电流经历两次先增大后减小 | |
| C. | 水平拉力方向与速度同向 | |
| D. | 水平拉力方向与速度方向无关 |
 如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )
如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )| A. | 加速度始终增大 | B. | 加速度先增大后减小 | ||
| C. | 速度先增大后减小 | D. | 速度一直减小 |
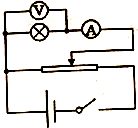 标有“6V,1.5W”的小灯泡,为了测量其0~6V不同电压下的实际功率,提供的器材除导线和开关外,还有:
标有“6V,1.5W”的小灯泡,为了测量其0~6V不同电压下的实际功率,提供的器材除导线和开关外,还有: