题目内容
(2011?湖南一模)如图甲所示,在边界MN左侧存在斜方向的匀强电场E1,在MN的右侧有竖直向上、场强大小为E2=0.4N/C的匀强电场,还有垂直纸面向内的匀强磁场B(图甲中未画出)和水平向右的匀强电场E3(图甲中未画出),B和E3随时间变化的情况如图乙所示,P1P2为距MN边界2.295m的竖直墙壁,现有一带正电微粒质量为4×10-7kg,电量为1×10-5C,从左侧电场中距MN边界
m的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设此时刻t=0,取g=10m/s2.求:
(1)MN左侧匀强电场的电场强度E1的大小和方向(sin37°=0.6);
(2)带电微粒在MN右侧场区中运动了1.5s时的速度;
(3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(
≈0.19)

| 1 |
| 15 |
(1)MN左侧匀强电场的电场强度E1的大小和方向(sin37°=0.6);
(2)带电微粒在MN右侧场区中运动了1.5s时的速度;
(3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(
| 1.2 |
| 2π |

分析:(1)粒子做直线运动,故重力和电场力的合力与速度方向在一条直线上,故电场力向右上方,与电场线同方向,然后对直线加速过程运用运动学公式求解出加速度,再根据牛顿第二定律列式分析求解;
(2)带电微粒在MN右侧场区中,重力和向上的电场力平衡,故在第1秒内直线加速,根据牛顿第二定律求出加速度,再根据运动学公式求解末速度,后0.5s内做匀速圆周运动,速度大小不变;
(3)带电微粒在MN右侧场区中运动过程中,第1秒向右直线加速,接下来的半秒做匀速匀速圆周运动,再接下来的1秒向左直线加速,再下来的半秒做匀速匀速圆周运动,直到与墙壁碰撞为止,根据牛顿第二定律和运动学公式列式联立求解即可.
(2)带电微粒在MN右侧场区中,重力和向上的电场力平衡,故在第1秒内直线加速,根据牛顿第二定律求出加速度,再根据运动学公式求解末速度,后0.5s内做匀速圆周运动,速度大小不变;
(3)带电微粒在MN右侧场区中运动过程中,第1秒向右直线加速,接下来的半秒做匀速匀速圆周运动,再接下来的1秒向左直线加速,再下来的半秒做匀速匀速圆周运动,直到与墙壁碰撞为止,根据牛顿第二定律和运动学公式列式联立求解即可.
解答:解:(1)设MN左侧匀强电场场强为E1,方向与水平方向夹角为θ
带电小球受重力和电场力,由于粒子做直线运动,故电场力向右上方
沿水平方向有 qE1cosθ=ma
沿竖直方向有 qE1sinθ=mg
对水平方向的匀加速运动,根据速度位移公式,有
v2=2as
代入数据可解得
E1=0.5N/C
θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在MN右侧场区始终满足 qE2=mg
在0~1s时间内,带电微粒在E3电场中 a=
=
=0.1m/s2
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s
在1~1.5s时间内,带电微粒在磁场B中运动,
周期为 T=
=
=1s
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动;
故带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s~1s时间内带电微粒前进距离 s1=vt+
at2=1×1+
×0.1×12=1.05m
带电微粒在磁场B中作圆周运动的半径 r=
=
=
m
因为r+s1<2.28m,所以在1s~2s时间内带电微粒未碰及墙壁
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2,
在3s内带电微粒共前进距离
s3=vt3+
at32=1×2+
×0.1×22=2.2m
在3s时带电微粒的速度大小为 v3=v+at3=1+0.1×2=1.2m/s
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径r3=
=
=
m=0.19m
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁
带电微粒在3s以后运动情况如右图,其中 d=2.295-2.2=0.095m
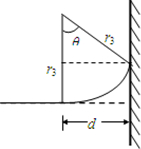
sinθ=
=0.5,θ=30°
所以,带电微粒作圆周运动的时间为t3=
=
=
=
s
故带电微粒与墙壁碰撞的时间为 t总=3+
=
s.
带电小球受重力和电场力,由于粒子做直线运动,故电场力向右上方
沿水平方向有 qE1cosθ=ma
沿竖直方向有 qE1sinθ=mg
对水平方向的匀加速运动,根据速度位移公式,有
v2=2as
代入数据可解得
E1=0.5N/C
θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在MN右侧场区始终满足 qE2=mg
在0~1s时间内,带电微粒在E3电场中 a=
| qE3 |
| m |
| 1×10-5×0.004 |
| 4×10-7 |
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s
在1~1.5s时间内,带电微粒在磁场B中运动,
周期为 T=
| 2πm |
| qB |
| 2π×4×10-7 |
| 1×10-5×0.08π |
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动;
故带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s~1s时间内带电微粒前进距离 s1=vt+
| 1 |
| 2 |
| 1 |
| 2 |
带电微粒在磁场B中作圆周运动的半径 r=
| mv |
| qB |
| 4×10-7×1.1 |
| 1×10-5×0.08π |
| 1.1 |
| 2π |
因为r+s1<2.28m,所以在1s~2s时间内带电微粒未碰及墙壁
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2,
在3s内带电微粒共前进距离
s3=vt3+
| 1 |
| 2 |
| 1 |
| 2 |
在3s时带电微粒的速度大小为 v3=v+at3=1+0.1×2=1.2m/s
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径r3=
| mv3 |
| qB |
| 4×10-7×1.2 |
| 1×10-5×0.08π |
| 1.2 |
| 2π |
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁
带电微粒在3s以后运动情况如右图,其中 d=2.295-2.2=0.095m

sinθ=
| d |
| r3 |
所以,带电微粒作圆周运动的时间为t3=
| T3 |
| 12 |
| 2πm |
| 12qB |
| 2π×4×10-7 |
| 12×1×10-5×0.08π |
| 1 |
| 12 |
故带电微粒与墙壁碰撞的时间为 t总=3+
| 1 |
| 12 |
| 37 |
| 12 |
点评:本题关键分析清楚粒子的运动规律,然后分阶段运用牛顿第二定律、向心力公式和运动学公式列式求解.

练习册系列答案
相关题目
 (2011?湖南一模)如图所示,小车上固定着硬杆,杆的端点固定着一个质量为m的小球.当小车有水平向右的加速度且逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的(00′沿杆方向)(
(2011?湖南一模)如图所示,小车上固定着硬杆,杆的端点固定着一个质量为m的小球.当小车有水平向右的加速度且逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的(00′沿杆方向)( (2011?湖南一模)如图所示为牵引力F和车速倒数
(2011?湖南一模)如图所示为牵引力F和车速倒数 (2011?湖南一模)如图所示电路中,三只灯泡原来都正常发光,当滑动变阻器的滑动触头P向右移动时,下面判断正确的是( )
(2011?湖南一模)如图所示电路中,三只灯泡原来都正常发光,当滑动变阻器的滑动触头P向右移动时,下面判断正确的是( ) (2011?湖南一模)“六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法正确的是( )
(2011?湖南一模)“六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法正确的是( )