题目内容
1. 如图所示,两条平行金属轨道相距L=1m,它有与水平方向成θ=30°的光滑倾斜导轨和粗糙的水平导轨两部分,水平导轨处于竖直向下的匀强磁场中,倾斜导轨ef与ab间有垂直于斜面向下的匀强磁场,磁感应强度大小为B1=1T.现将两金属棒MN和PQ分别置于水平导轨上和倾斜导轨的磁场区内,由静止释放,棒PQ沿导轨下滑,棒MN始终静止.已知两棒的质量均为m=0.1kg,电阻均为R=2Ω,棒MN与水平导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,两棒均与导轨垂直且接触良好,倾斜导轨有磁场区与无磁场区均足够长,不计导轨的电阻,重力加速度为g=10m/s2.
如图所示,两条平行金属轨道相距L=1m,它有与水平方向成θ=30°的光滑倾斜导轨和粗糙的水平导轨两部分,水平导轨处于竖直向下的匀强磁场中,倾斜导轨ef与ab间有垂直于斜面向下的匀强磁场,磁感应强度大小为B1=1T.现将两金属棒MN和PQ分别置于水平导轨上和倾斜导轨的磁场区内,由静止释放,棒PQ沿导轨下滑,棒MN始终静止.已知两棒的质量均为m=0.1kg,电阻均为R=2Ω,棒MN与水平导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,两棒均与导轨垂直且接触良好,倾斜导轨有磁场区与无磁场区均足够长,不计导轨的电阻,重力加速度为g=10m/s2.(1)求棒PQ下滑最大速度的大小;
(2)求棒PQ由静止释放到速度达到最大过程中,通过棒MN某横截面的电荷量q=0.5C,求该过程整个回路中产生的总焦耳热;
(3)若将棒PQ在ef上方与ef相距x的地方由静止释放,要使MN始终静止,求水平导轨处磁感应强度的最大值B2与x之间的关系.
分析 (1)PQ棒先向下做加速度减小的变加速运动,后做匀速直线运动,速度达到最大.由法拉第定律、欧姆定律推导出安培力与速度的关系式,再由平衡条件求解最大速度.
(2)由法拉第电磁感应定律、欧姆定律和电流的定义式结合求解棒PQ下滑的距离,再由能量守恒定律求焦耳热.
(3)要使MN始终静止,PQ速度最大时也必须静止,由
解答 解:(1)设棒PQ下滑最大速度的大小为vm.棒PQ的速度最大时做匀速直线运动.
由 E=B1Lvm,I=$\frac{E}{2R}$,F安=B1IL,得:
F安=$\frac{{B}_{1}^{2}{L}^{2}{v}_{m}}{2R}$
棒PQ匀速运动时有:F安=mgsinθ
联立得 vm=$\frac{2mgRsinθ}{{B}_{1}^{2}{L}^{2}}$=$\frac{2×0.1×10×2×0.5}{{1}^{2}×{1}^{2}}$=2m/s
(2)棒PQ由静止释放到速度达到最大过程中下滑的距离为s.通过棒MN某横截面的电荷量为:
q=$\overline{I}$t=$\frac{{B}_{1}L\overline{v}t}{2R}$=$\frac{{B}_{1}Ls}{2R}$
则有:s=$\frac{2qR}{BL}$=$\frac{2×0.5×2}{1×1}$=2m
根据能量守恒定律得整个回路中产生的总焦耳热为:
Q=mgssinθ-$\frac{1}{2}m{v}_{m}^{2}$=0.1×10×0.5-$\frac{1}{2}$×0.1×22=0.3J
(3)将棒PQ在ef上方与ef相距x的地方由静止释放,到达ef时的速度为:
v=$\sqrt{2ax}$=$\sqrt{2gsin30°•x}$=$\sqrt{gx}$
PQ棒刚进入磁场时产生的感应电流为:
I=$\frac{{B}_{1}Lv}{2R}$
要使MN始终静止,则有:B2IL≤μmg
联立得:
B2≤$\frac{2μmgR}{{B}_{1}{L}^{2}\sqrt{gx}}$=$\frac{2×0.5×0.1×10×2}{1×{1}^{2}×\sqrt{10x}}$=$\sqrt{\frac{2}{5x}}$
答:(1)棒PQ下滑最大速度的大小是2m/s.
(2)该过程整个回路中产生的总焦耳热是0.3J.
(3)水平导轨处磁感应强度的最大值B2与x之间的关系为B2≤$\sqrt{\frac{2}{5x}}$.
点评 本题是双杆类型,分别研究它们运动过程和状态是基础,运用力学和电路、电磁感应的规律研究MN棒,对于感应电荷量,要熟悉一般表达式q=$\frac{△Φ}{R+r}$,知道电量可求导体棒的位移.

 阶梯计算系列答案
阶梯计算系列答案| A. | “非”门 | B. | “或”门 | C. | “与”门 | D. | “与非”门 |
| A. | 滑动摩擦力一定做负功 | |
| B. | 静摩擦力一定不做功 | |
| C. | 静摩擦力可能做功 | |
| D. | 两物体间相互作用的一对摩擦力做功的总和恒等于零 |
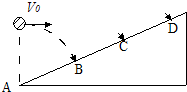 如图所示,一小球以v0水平速度向斜面抛出,落于B点,AB=BC=CD若将小球以2v0从同一点水平抛出,则小球将落到位置是( )
如图所示,一小球以v0水平速度向斜面抛出,落于B点,AB=BC=CD若将小球以2v0从同一点水平抛出,则小球将落到位置是( )| A. | C点 | B. | CD之间 | C. | BC之间 | D. | 无法确定 |
| A. | 偏高 | B. | 偏低 | C. | 相同 | D. | 无法判断 |
| A. | 曲线运动一定是变速运动 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 匀速圆周运动一定是变加速运动 | |
| D. | 加速度、速度都不变的运动是直线运动 |
 如图所示,用伏安法测电阻.电压表的内电阻为2.0×103Ω,电流表的内电阻为1.0×10-2Ω.已知电压表的读数为20V,电流表读数为0.4A,则待测电阻RX的测量值为50Ω,其真实值应该为51.3Ω.
如图所示,用伏安法测电阻.电压表的内电阻为2.0×103Ω,电流表的内电阻为1.0×10-2Ω.已知电压表的读数为20V,电流表读数为0.4A,则待测电阻RX的测量值为50Ω,其真实值应该为51.3Ω. 如图所示,起重机将货物沿竖直方向匀加速吊起,同时又沿横梁水平匀速向右运动.此时,站在地面上观察,货物运动的轨迹可能是下图中的哪一个?( )
如图所示,起重机将货物沿竖直方向匀加速吊起,同时又沿横梁水平匀速向右运动.此时,站在地面上观察,货物运动的轨迹可能是下图中的哪一个?( )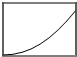



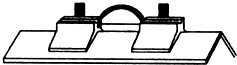 在用气垫导轨做“探究碰撞中的不变量”实验时,左侧滑块质量m1=170g,右侧滑块质量m2=110g,挡光片宽度为3.00cm,两滑块之间有一压缩的弹簧片,并用细线连在一起,如图所示.开始时两滑块静止,烧断细线后,两滑块分别向左、右方向运动.挡光片通过光电门的时间分别为△t1=0.32s,△t2=0.21s.则两滑块的速度分别为v1′=0.09m/s,v2′=0.143m/s.烧断细线前m1v1+m2v2=0kg•m/s,烧断细线后m1v1′+m2v2′=0kg•m/s.可得到的结论是系统动量守恒.
在用气垫导轨做“探究碰撞中的不变量”实验时,左侧滑块质量m1=170g,右侧滑块质量m2=110g,挡光片宽度为3.00cm,两滑块之间有一压缩的弹簧片,并用细线连在一起,如图所示.开始时两滑块静止,烧断细线后,两滑块分别向左、右方向运动.挡光片通过光电门的时间分别为△t1=0.32s,△t2=0.21s.则两滑块的速度分别为v1′=0.09m/s,v2′=0.143m/s.烧断细线前m1v1+m2v2=0kg•m/s,烧断细线后m1v1′+m2v2′=0kg•m/s.可得到的结论是系统动量守恒.