题目内容
已知一物体做加速直线运动，依次通过A、B、C三个位置，如图所示．B为AC的中点，物体在AB段加速度为a1，在BC段加速度为a2，现测得VB=| VA+VC | 2 |
分析：由vB=
，得出vB-vA=vC-vB，结合匀变速直线运动的速度位移公式或速度时间公式求出加速度的比值，从而比较出加速度的大小．
| vA+vC |
| 2 |
解答：解法1：由vB=
得，vB-vA=vC-vB …①
AB段匀加速：vB2-vA2=2a1sAB …②
BC段匀加速：vC2-vB2=2a2sBC …③
可得：
=
由于物体一直做加速直线运动，则vB+vC＞vA+vB 所以 a1＜a2．
解法2：
依题意知：a1=
，a2=
因为vB=
，则vB-vA=vC-vB
则有
=
物体一直做加速，连续相邻相等位移内平均速度变大，则tAB＞tBC．
所以a1＜a2．
答：AB段的加速度小于BC段的加速度．
| vA+vC |
| 2 |
AB段匀加速：vB2-vA2=2a1sAB …②
BC段匀加速：vC2-vB2=2a2sBC …③
可得：
| vA+vB |
| vB+vC |
| a1 |
| a2 |
由于物体一直做加速直线运动，则vB+vC＞vA+vB 所以 a1＜a2．
解法2：
依题意知：a1=
| vB-vA |
| tAB |
| vC-vB |
| tBC |
因为vB=
| vA+vC |
| 2 |
则有
| a1 |
| a2 |
| tBC |
| tAB |
物体一直做加速，连续相邻相等位移内平均速度变大，则tAB＞tBC．
所以a1＜a2．
答：AB段的加速度小于BC段的加速度．
点评：解决本题的关键掌握匀变速直线运动的运动学公式和推论，并能灵活运用．
练习册系列答案
相关题目
。试由此推导出两加速度大小的关系。（要求用两种不同解法求解）
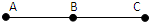已知一物体做加速直线运动，依次通过A、B、C三个位置，如图所示．B为AC的中点，物体在AB段加速度为a1，在BC段加速度为a2，现测得VB=
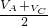．试由此推导出两加速度大小的关系．（要求用两种不同解法求解，）