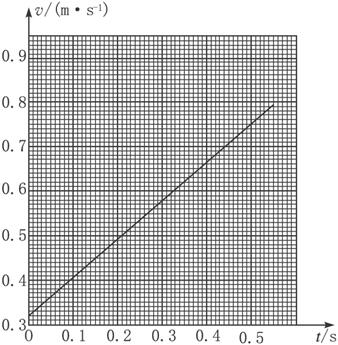
题目内容
如图10-3-6所示为一列简谐波在两个不同时刻的图象,虚线为实线在Δt=0.5 s后的图象.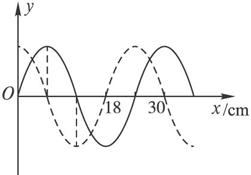
图10-3-6
(1)若波向右传播,且T<Δt<3T,求波速;
(2)若波速v=0.6 m/s,判断v的方向.
解析:(1)求波速的方法有两种:①找出Δt=0.5 s内波传播的距离s,由v=![]() 求得.②由图象读得波长λ,并找出Δt与T的关系,从而求出T,再由v=
求得.②由图象读得波长λ,并找出Δt与T的关系,从而求出T,再由v=![]() 求得.这里采用方法①来解答.
求得.这里采用方法①来解答.
由图象和波动的周期性知Δt内,波传过的距离的可能值s=nλ+![]() λ,其中n=0,1,2,3,….由图象得λ=0.24 m.
λ,其中n=0,1,2,3,….由图象得λ=0.24 m.
已知T<Δt<3T,故λ 所以s1=1 v1= 或v2= (2)由s=v·Δt=0.6×0.5 m=0.3 m=0.24 m+0.06 m,即将实线波形平移 答案:(1)0.84 m/s或1.32 m/s (2)向左![]() λ=0.42 m或s2=2
λ=0.42 m或s2=2![]() λ=0.66 m
λ=0.66 m![]() m/s=0.84 m/s
m/s=0.84 m/s![]() m/s=1.32 m/s.
m/s=1.32 m/s.![]() λ=0.06 m,便与虚线波形重合,所以波应向左传播.
λ=0.06 m,便与虚线波形重合,所以波应向左传播.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目