Question

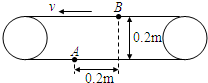
两个直径均为0.2m的轮逆时针方向匀速转动，带动传送带匀速运动．在传送带的水平部分有A、B两个标记点．某时刻A、B位置关系如图所示，A、B之间的水平距离为0.2m，此时有一原先附着在传送带下B点的水滴与B点脱离而落下，最后恰好掉在A点．试求此传送带的传送速度v．
某同学解法如下：B点的水滴掉落后自由下落0.2m，时间为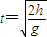…①
在水滴下落过程中A点前进0.2m则正好与水滴相遇，s=vt…②
得v=1m/s．经检查，计算无误．
该同学的分析过程存在一个错误，请指出该错误并改正后再求出正确结果．

Answer 1

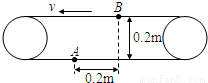
【答案】分析：B点的水滴掉落后不是自由下落，而是向左做平抛运动．根据平抛运动的规律，抓住水滴的水平位移以及传送带向前运动的位移之和等于0.2m，求出传送带的速度．
解答：解：B点的水滴掉落后不是自由下落，而是向左做平抛运动．      
下落时间：
这段时间内：水滴向左的水平位移：x_B=vt=0.2v
A点向右的水平位移：x_A=vt=0.2v
而x_A+x_B=AB即0.2v+0.2v=0.2
解得v=0.5m/s
答：传送带的传送速度为0.5m/s．
点评：解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式灵活求解．