题目内容
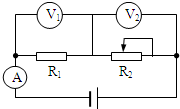
 (17分)如图所示的电路中,各电源的内阻均为零,其中B、C两点与其右方由1.0W的电阻和2.0W的电阻构成的无穷组合电路相接。求图中10mF的电容器与E点相接的极板上的电荷量。
(17分)如图所示的电路中,各电源的内阻均为零,其中B、C两点与其右方由1.0W的电阻和2.0W的电阻构成的无穷组合电路相接。求图中10mF的电容器与E点相接的极板上的电荷量。
解析:
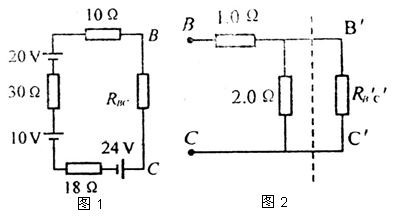
设B、C右方无穷组合电路的等效电阻为RBC,则题图中通有电流的电路可以简化为图1中的电路。B、C右方的电路又可简化为图2的电路,其中![]() 是虚线右方电路的等效电阻。由于B¢、C¢右方的电路与B、C右方的电路结构相同,而且都是无穷组合电路,故有
是虚线右方电路的等效电阻。由于B¢、C¢右方的电路与B、C右方的电路结构相同,而且都是无穷组合电路,故有
![]() (1)
(1)
由电阻串、并联公式可得
![]() (2)
(2)
由式(1)、(2)两式得
![]()
解得
RBC=2.0 W (3)
图1所示回路中的电流为
![]() (4)
(4)
电流沿顺时针方向。
设电路中三个电容器的电容分别为C1、C2和C3,各电容器极板上的电荷分别为Q1、Q2和Q3,极性如图3所示。由于电荷守恒,在虚线框内,三个极板上电荷的代数和应为零,即
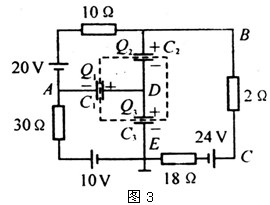
Q1+Q2-Q3=0 (5)
A、E两点间的电势差
![]() (6)
(6)
又有
![]() (7)
(7)
B、E两点间的电势差
![]() (8)
(8)
又有
![]() (9)
(9)
根据(5)、(6)、(7)、(8)、(9)式并代入C1、C2和C3之值后可得
Q3=1.3×10-4C (10)
即电容器C3与E点相接的极板带负电,电荷量为1.3×10-4C。
评分标准:
本题17分.求得(3)式给3分,(4)式1分,(5)、(6)、(7)、(8)、(9)、(10)式各2分,指出所考察的极板上的电荷是负电荷再给1分。

 阅读快车系列答案
阅读快车系列答案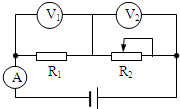 如图所示的电路中,各电表为理想电表,电源内阻不能忽略,当滑动变阻器R2的滑动头从某位置向左移动一小段距离的过程中,设V1、V2、A的读数分别是U1、U2、I;V1、V2、A读数的变化量分别为△U1、△U2、△I,则下列说法正确的是( )
如图所示的电路中,各电表为理想电表,电源内阻不能忽略,当滑动变阻器R2的滑动头从某位置向左移动一小段距离的过程中,设V1、V2、A的读数分别是U1、U2、I;V1、V2、A读数的变化量分别为△U1、△U2、△I,则下列说法正确的是( )