题目内容
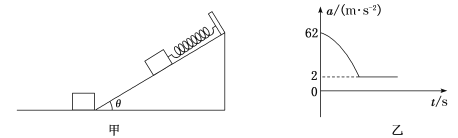
【题目】如图甲所示，倾角θ=37°的粗糙斜面固定在水平面上，斜面上端固定一轻质弹簧，下端与一足够长的水平面平滑相连，水平面右端放置一个质量M=7.0kg的滑块，开始时弹箦被一质量m=1.0kg的小物块（可视为质点）压缩，小物块与弹簧只接触不相连，此时小物块距斜面底端的距离
=4.0m。t=0时释放小物块，图乙为小物块在斜面上运动的加速度a随时间t变化的部分图象，小物块到达水平面并与滑块发生弹性碰撞（碰撞时间极短）。已知弹簧的劲度系数k=75N/m，弹性势能的表达式为
，x为弹簧形变量，所有接触面之间动摩擦因数均相同。g取10m/s2，sin37°=0.6，cos37°=0.8。最大静摩擦力等于滑动摩擦力。求：
(1)斜面与小物块之间的动摩擦因数μ；
(2)小物块到达斜面底端时的速度大小；
(3)滑块运动的路程s。
【答案】(1)0.5；(2)
；(3)
【解析】
(1)由题图乙可知，当小物块与弹簧分离后，小物块沿斜面向下做匀加速直线运动，加速度的大小为
根据牛顿第二定律有
解得
(2)由题图乙可知，
时加速度的大小为
设此时弹簧压缩量为x，根据牛顿第二定律有
解得
设小物块到达斜面底端的速度为
，由动能定理得
解得
(3)在斜面底端，小物块与滑块发生第一次弹性碰撞，设碰后小物块的速度为
，滑块的速度为
，则
解得
第一次碰撞后，滑块向左做匀减速运动，经过
停下来，发生的位移为
，则
解得
小物块冲上斜面又滑下来，沿斜面向上运动的加速度为
位移为
解得
所以发生第二次碰撞时滑块已经静止，小物块没有接触弹簧但速度已经减为零，随后加速下滑。设小物块刚要与滑块二次碰撞时的速度为
，根据动能定理
，
解得
小物块与滑块发生第二次弹性碰撞，碰后小物块的速度为
，滑块的速度为
，
则
，
解得
第二次碰撞后，滑块向左做匀减速运动，发生的位移为
，则
小物块向右做匀减速运动，发生的位移为
不能发生第三次碰撞，所以滑块的总路程
