题目内容
如图所示，在斜面顶端a处以大小为va的水平速度抛出一小球，经过时间ta恰好落在斜面底端P处；今在P点正上方与a等高的b处以大小为vb的水平速度抛出另一小球，经过时间tb恰好落在斜面的中点处．若不计空气阻力，下列关系式正确的是（ ）分析：ab两处抛出的小球都做平抛运动，由平抛运动的规律水平方向上的匀速直线运动，和竖直方向上的自由落体运动来分析求解．
解答：解：做平抛运动的物体运动时间由竖直方向的高度决定 t=
，a物体下落的高度是b的2倍，所以有ta=
tb，所以D正确；
设斜面的夹角为θ，则ap的水平距离L=
，
则有 va=
=
=
，
同理可得 vb=
=
=
，
两式相比可得，va=
vb，所以B正确．
故选BD．
|
| 2 |
设斜面的夹角为θ，则ap的水平距离L=
| h |
| tanθ |
则有 va=
| L |
| ta |
| h |
| ta?tanθ |
| h | ||
|
同理可得 vb=
| L |
| tb |
| ||
| tb?tanθ |
| h |
| 2tb?tanθ |
两式相比可得，va=
| 2 |
故选BD．
点评：本题就是对平抛运动规律的考查，平抛运动可以分解为在水平方向上的匀速直线运动，和竖直方向上的自由落体运动来求解．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
（2007?宝坻区一模）如图所示，在斜面顶端的A点以速度v平抛一小球经t1时间落到斜面上B点处，若在A点将此小球以速度0.5v水平抛出，经t2落到斜面上的C点处，以下判断正确的是（ ）
（2006?连云港一模）十七世纪七十年代，英国赛斯特城的主教约翰?维尔金斯设计了一种磁力“永动机”，其结构如图所示：在斜面顶端放一块强磁铁M，斜面上、下端各有一个小孔P、Q，斜面下有一个连接两小孔的弯曲轨道．维尔金斯认为：如果在斜坡底放一个铁球，那么在磁铁的引力作用下，铁球会沿斜面向上运动，当球运动到P孔时，它会漏下，再沿着弯曲轨道返回到Q，由于这时球具有速度可以对外做功．然后又被磁铁吸引回到上端，到P处又漏下…对于这个设计，下列判断中正确的是（ ）
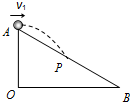如图所示，在斜面顶端A以速度v1水平抛出一小球，经过时间t1恰好落在斜面的中点P；若在A以速度v2水平抛出小球，经过时间t2小球落在斜面底端B．不计空气阻力，下列判断正确的是（ ）| A、v2=2v1 | B、v2＜2v1 | C、t2=2t1 | D、t2＜2t1 |
如图所示，在斜面顶端的A点以速度v平抛一小球经t1时
：1?