题目内容
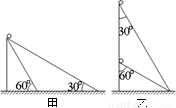
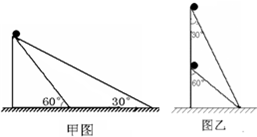
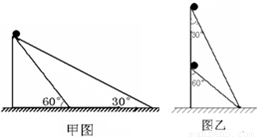
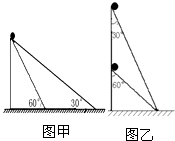 某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )
某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )分析:对小球进行受力分析,根据牛顿第二定律求出加速度,再根据匀加速直线运动位移-时间公式求出时间.
解答:解:A、在甲图中:
对小球进行受力分析,受到重力和支持力,合力提供加速度,根据牛顿第二定律可知:
运动的加速度为a=gsinθ
设高度为h,则斜面的长度为
根据匀加速直线运动,位移-时间公式可知:
=
at2
t=
甲图中两个斜面倾角不等,故小球在两个斜面上运动的时间不相同,故A错误;
B、下滑到斜面底端时速度为:v=at=
故B正确
C、在乙图中:
对小球进行受力分析,受到重力和支持力,合力提供加速度,根据牛顿第二定律可知:
运动的加速度为a=gcosθ
两个斜面倾角不等,所以加速度不相同,
设底边长为h,则斜面的长度为
根据匀加速直线运动,位移-时间公式可知:
=
at2
t=
当θ分别为30°和60°时,sinθcosθ相等,故时间相等,D正确.
速度为v=at=
故C错误
故选BC.
对小球进行受力分析,受到重力和支持力,合力提供加速度,根据牛顿第二定律可知:
运动的加速度为a=gsinθ
设高度为h,则斜面的长度为
| h |
| sinθ |
根据匀加速直线运动,位移-时间公式可知:
| h |
| sinθ |
| 1 |
| 2 |
t=
|
甲图中两个斜面倾角不等,故小球在两个斜面上运动的时间不相同,故A错误;
B、下滑到斜面底端时速度为:v=at=
|
故B正确
C、在乙图中:
对小球进行受力分析,受到重力和支持力,合力提供加速度,根据牛顿第二定律可知:
运动的加速度为a=gcosθ
两个斜面倾角不等,所以加速度不相同,
设底边长为h,则斜面的长度为
| h |
| sinθ |
根据匀加速直线运动,位移-时间公式可知:
| h |
| sinθ |
| 1 |
| 2 |
t=
|
当θ分别为30°和60°时,sinθcosθ相等,故时间相等,D正确.
速度为v=at=
|
故C错误
故选BC.
点评:该题主要考查了牛顿第二定律及匀变速直线运动位移-时间公式的应用,注意几何知识在物理解题过程中的应用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
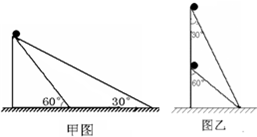 某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )
某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )