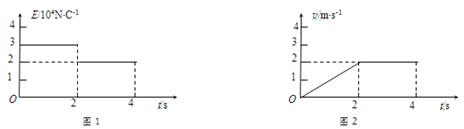题目内容
【题目】如图所示，竖直平面MN与纸面垂直，MN右侧的空间存在着垂直纸面向内的匀强磁场和水平向左的匀强电场，MN左侧的水平面光滑，右侧的水平面粗糙．质量为m的物体A静止在MN左侧的水平面上，已知该物体带负电，电荷量的大小为为q．一质量为
的不带电的物体B以速度v0冲向物体A并发生弹性碰撞，碰撞前后物体A的电荷量保持不变．求：
（1）碰撞后物体A的速度大小；
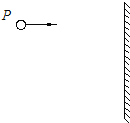
（2）若A与水平面的动摩擦因数为μ，重力加速度的大小为g，磁感应强度的大小为
，电场强度的大小为
．已知物体A从MN开始向右移动的距离为
时，速度增加到最大值．求：
a．此过程中物体A克服摩擦力所做的功W；
b．此过程所经历的时间t．
【答案】（1）
（2）a. 
b. 
【解析】试题分析：（1）设A、B碰撞后的速度分别为vA、vB，由于A、B发生弹性碰撞，动量、动能守恒，则有：
①
②
联立①②可得： 
③
（2）a．A的速度达到最大值vm时合力为零，受力如图所示。
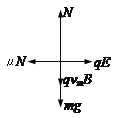
竖直方向合力为零，有： 
④
水平方向合力为零，有： 
⑤
根据动能定理，有： 
⑥
联立③④⑤⑥并代入相相关数据可得： 
b．方法一：
在此过程中，设A物体运动的平均速度为
，根据动量定理有：
⑦
⑧
依题意有： 
⑨
联立③④⑤⑦⑧⑨并代入相关数据可得： 
方法二：设任意时刻A物体运动的速度为v，取一段含此时刻的极短时间Δt，设此段时间内速度的改变量为Δv，根据动量定理有：
⑦
而
⑧
⑨
联立③④⑤⑦⑧⑨并代入相关数据可得： 
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
