题目内容
【题目】如图所示，一轻质弹簧下端与固定挡板相连，上端与放在倾角θ=30°的光滑斜面上的小车A相接触（未连接）．小车A质量M=3kg，内有质量m0=1kg的砝码，小车A又与一跨过定滑轮的不可伸长的轻绳一端相连，绳另一端悬挂着物体B ， B的下面又挂着物体C ， B和C质量均为m=1kg，A、B、C均处于静止状态．现剪断B和C之间的绳子，则A和B开始做振幅为d=5cm的简谐运动，斜面足够长且始终静止．（g取10m/s2）试求：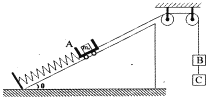
（1）剪断绳子的瞬间小车A的加速度大小；
（2）剪断绳子后弹簧的最大弹性势能；
（3）当小车A运动到最低点时，取走小车内的砝码，此后小车A沿斜面上滑的最大距离．
【答案】
（1）
绳子剪短前，由于（M+m0）gsin30°=2mg，弹簧没有弹力，弹簧没有弹力．
绳子剪短瞬间：
对A受力分析得：(M+m0)gsin30° -T=(M+m)a①
对B受力分析得：T-mg=ma ②
联立①②解得：a=2m/s2．
故剪断绳子的瞬间小车A的加速度大小为2m/s2
（2）
当弹簧被压缩2d时弹性势能最大，由功能关系得：
（M+m）g×2dsin30°=mg×2d+Epm
解得：EPm=1J
故剪断绳子后弹簧的最大弹性势能EPm=1J
（3）
当小车滑行道最高点时，A、B的速度均为0，由系统功能关系得：
Epm=Mgssin300-mgs
解得：s=0.2m．
故此后小车A沿斜面上滑的最大距离为0.2m．
【解析】（1）绳子剪短前，由于（M+m0）gsin30°=2mg ， 弹簧没有弹力，弹簧没有弹力．
绳子剪短瞬间：
对A受力分析得：(M+m0)gsin30° -T=(M+m)a①
对B受力分析得：T-mg=ma ②
联立①②解得：a=2m/s2 ．
故剪断绳子的瞬间小车A的加速度大小为2m/s2 ． （2）当弹簧被压缩2d时弹性势能最大，由功能关系得：
（M+m）g×2dsin30°=mg×2d+Epm
解得：EPm=1J
故剪断绳子后弹簧的最大弹性势能EPm=1J．（3）当小车滑行道最高点时，A、B的速度均为0，由系统功能关系得：
Epm=Mgssin300-mgs
解得：s=0.2m．
故此后小车A沿斜面上滑的最大距离为0.2m．
【考点精析】根据题目的已知条件，利用机械能守恒及其条件的相关知识可以得到问题的答案，需要掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变．
